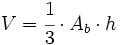Áreas y volúmenes
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 21:08 15 oct 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 21:13 15 oct 2007 Coordinador (Discusión | contribuciones) (→Prisma) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| {{Tabla3 | {{Tabla3 | ||
| |celda1= | |celda1= | ||
| - | [[Imagen:prismarecto.jpg]] | + | [[Imagen:prisma.gif]] |
| |celda2={{p}} | |celda2={{p}} | ||
| * '''Área:'''{{p}} | * '''Área:'''{{p}} | ||
| Línea 88: | Línea 88: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Pirámide== | ==Pirámide== | ||
| {{Tabla3 | {{Tabla3 | ||
Revisión de 21:13 15 oct 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Ejercicios | WIRIS Geogebra Calculadora |
Prisma
| Imagen:Prisma.gif |
|
|
|
Actividad Interactiva: Area y volumen del prisma
Actividad 1: Halla el área lateral y total de un prisma recto de base un triángulo equilátero, de 1 cm de lado y 2 cm de altura.
Actividad: Comprueba los resultados en la siguiente escena:
Actividad 2: Halla el volumen de un prisma recto de base cuadrada, de lado 1,5 cm y altura 2,2 cm...
Actividad: Comprueba los resultados en la siguiente escena: |
Ortoedro y cubo
Como sabemos, un ortoedro es un prisma recto de base rectangular o cuadrada y un caso particular de ortoedro es el cubo cuyas caras son todas cuadradas.
|
Actividad Interactiva: Area y volumen del ortoedro y cubo
Actividad 1: Halla el área lateral y total de un ortoedro de aristas 2, 3 y 1,5 cm.
Actividad: Comprueba los resultados en la siguiente escena:
Actividad 2: Halla el volumen de un cubo de 3 cm de arista.
Actividad: Comprueba los resultados en la siguiente escena: |
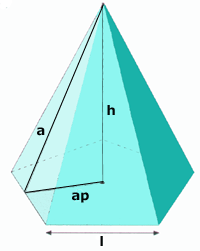
Pirámide
|
|
|
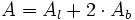
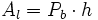
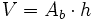
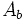 : Área de la base.
: Área de la base.
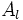 : Área lateral.
: Área lateral.
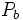 : Perímetro de la base.
: Perímetro de la base.
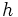 : altura.
: altura.
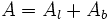
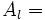 Suma de las áreas de los triángulos
Suma de las áreas de los triángulos