Los Números Reales (4ºESO-A)

De Wikipedia

Revisión de 08:43 28 may 2008 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior		Revisión actual Coordinador (Discusión | contribuciones) (→Conjuntos numéricos)
Línea 9:		Línea 9:
	{{Caja_Amarilla|texto=El conjunto formado por los números racionales y los irracionales se llama conjunto de los ''números reales'' y se designa por <math>\mathbb{R}</math>.}}		{{Caja_Amarilla|texto=El conjunto formado por los números racionales y los irracionales se llama conjunto de los ''números reales'' y se designa por <math>\mathbb{R}</math>.}}
	{{p}}		{{p}}
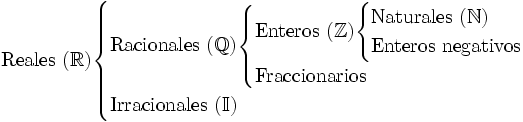
-	:<math>\begin{cases}	+	En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora:
-	\mathbb{R} & \mbox{Reales}	+
		+	<center>
		+	<math>
		+	\mbox{Reales } (\mathbb{R})
		+	\begin{cases}
		+	\mbox{Racionales }(\mathbb{Q})
	\begin{cases}		\begin{cases}
-	\mathbb{Q} & \mbox{Racionales}	+	\mbox{Enteros } (\mathbb{Z})
	\begin{cases}		\begin{cases}
-	\mathbb{Z} & \mbox{Enteros}	+	\mbox{Naturales } (\mathbb{N}) \\
-	\begin{cases}	+	\mbox{Enteros negativos}
-	\mathbb{N} & \mbox{Naturales} \\	+
-	& \mbox{Enteros negativos}	+
-	\end{cases}\\	+
-	& \mbox{Fraccionarios}	+
	\end{cases}\\		\end{cases}\\
-	\mathbb{I} & \mbox{Irracionales}	+	\mbox{Fraccionarios}
	\end{cases}\\		\end{cases}\\
-	\end{cases}	+	\mbox{Irracionales } (\mathbb{I})
		+	\end{cases}
	</math>		</math>
-		+	</center>
-		+
	[[Categoría: Matemáticas|Números]][[Categoría: Números|Reales]]		[[Categoría: Matemáticas|Números]][[Categoría: Números|Reales]]

---

Revisión actual

Conjuntos numéricos

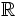En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora: