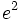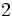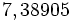Funciones exponenciales (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:08 25 ene 2009 Coordinador (Discusión | contribuciones) (→Función exponencial de base a) ← Ir a diferencia anterior |
Revisión de 14:13 25 ene 2009 Coordinador (Discusión | contribuciones) (→Función exponencial de base a) Ir a siguiente diferencia → |
||
| Línea 31: | Línea 31: | ||
| <center>'''a)''' <math>y = 2^x\;</math> (en verde);{{b4}}'''b)''' <math>y = 3^x\;</math> (en amarillo);{{b4}}'''c)''' <math>y = \left ( \frac{1}{2} \right )^x</math> (en rojo);{{b4}}'''d)''' <math>y = \left ( \frac{1}{3} \right )^x</math> (en turquesa)</center> | <center>'''a)''' <math>y = 2^x\;</math> (en verde);{{b4}}'''b)''' <math>y = 3^x\;</math> (en amarillo);{{b4}}'''c)''' <math>y = \left ( \frac{1}{2} \right )^x</math> (en rojo);{{b4}}'''d)''' <math>y = \left ( \frac{1}{3} \right )^x</math> (en turquesa)</center> | ||
| {{p}} | {{p}} | ||
| - | Comprueba en la siguiente escena las siguientes propiedades: | ||
| - | |||
| - | * Todas pasan por el punto (0,1). | ||
| - | * Si la base a>1, son crecientes y si 0<a<1 decrecientes. | ||
| - | * Son siempre positivas (su gráfica etá por encima del eje X). | ||
| - | * Observa como varía la gráfica al aumentar o disminuir el valor de la base. | ||
| - | * Las gráficas a) y c) son simétricas respecto del eje Y. Lo mismo ocurre con b) y d). | ||
| - | |||
| <center><iframe> | <center><iframe> | ||
| Línea 47: | Línea 39: | ||
| </iframe></center> | </iframe></center> | ||
| <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4h.html '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4h.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | {{p}} | ||
| + | |||
| + | Comprueba en la escena anterior las siguientes propiedades: | ||
| + | |||
| + | * Todas pasan por el punto <math>(0,1)\;</math> y <math>(a,0)\;</math>, donde <math>a\;</math> es la base. | ||
| + | * Si la base <math>a>1\;</math>, son crecientes y si <math>0<a<1\;</math> decrecientes. | ||
| + | * Son siempre positivas y nunca se anulan (su gráfica está por encima del eje X). | ||
| + | * Observa como varía la gráfica al aumentar o disminuir el valor de la base. | ||
| + | * Las gráficas a) y c) son simétricas respecto del eje Y. Lo mismo ocurre con b) y d). | ||
| {{p}} | {{p}} | ||
| Prueba a cambiar también las funciones por otras. No olvides pulsar "Intro" al cambiar cada función. | Prueba a cambiar también las funciones por otras. No olvides pulsar "Intro" al cambiar cada función. | ||
| Línea 52: | Línea 53: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | |||
| ===Propiedades=== | ===Propiedades=== | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
Revisión de 14:13 25 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Función exponencial de base a
Sea 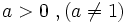 un número real. Se define la función exponencial de base
un número real. Se define la función exponencial de base  como:
como:
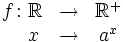
La función de base e (número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
|
Actividad Interactiva: Función exponencial
Actividad 1. Representación gráfica de distintas funciones exponenciales.
Actividad: En esta escena tienes las gráfica de las funciones: a)
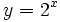 (en verde); b) (en verde); b) 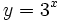 (en amarillo); c) (en amarillo); c) 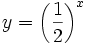 (en rojo); d) (en rojo); d) 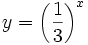 (en turquesa) (en turquesa)Comprueba en la escena anterior las siguientes propiedades:
|
Propiedades
Las funciones exponenciales cumplen las siguientes propiedades:
- Son continuas en
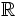 .
.
- Pasan por (0,1) y (1,a).
- Si a>1 son crecientes y si 0<a<1 son decrecientes. Su crecicmiento supera al de cualquier función potencia.
- Son positivas y nunca se anulan (su gráfica está por encima del eje X).
Calculadora
Exponencial de base 10
|
Calculadora: Exponencial de base 10 |
Exponencial de base e
|
Calculadora: Exponencial de base e |
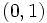 y
y 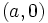 , donde
, donde 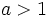 , son crecientes y si
, son crecientes y si 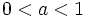 decrecientes.
decrecientes.
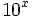 usaremos la tecla
usaremos la tecla 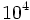
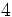
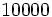
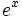 usaremos la tecla
usaremos la tecla