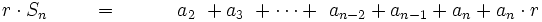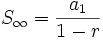Plantilla:Progresiones geométricas

De Wikipedia

(Diferencia entre revisiones)

Revisión de 12:10 27 sep 2014

Tabla de contenidos

1 Progresiones geométricas

Progresiones geométricas

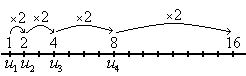
Una progresión geométrica es una sucesión de números en la que cada término se obtiene multiplicando el anterior por una cantidad fija, 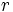$r\;\!$ , que llamaremos razón

Por ejemplo:

es una progresión geométrica de razón r=2.

Término general de una progresión geométrica

Término general de una progresión geométrica

Sean 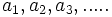$a_1, a_2, a_3, ..... \;\!$ términos de una progresión geométrica de razón $r\;\!$ .

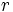Entonces se cumple que:

$a_n = a_1 \cdot r^{n-1}$

Demostración:

En efecto, razonando por inducción:

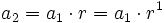
$a_2 = a_1 \cdot r = a_1 \cdot r^1 \;\!$

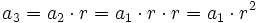
$a_3 = a_2 \cdot r = a_1 \cdot r \cdot r = a_1 \cdot r^2 \;\!$

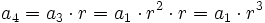
$a_4 = a_3 \cdot r = a_1 \cdot r^2 \cdot r = a_1 \cdot r^3 \;\!$

........................

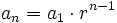
$a_n = a_1 \cdot r^{n-1}$

Videotutoriales sobre progesiones geométricas

Progresiones geométricas (11'41") Sinopsis:

Definición de progresión geométrica.
Ejemplos.
Término general de una progresión geométrica.

Ejercicio (4'17") Sinopsis:

Videotutorial

2 ejercicios (6'04") Sinopsis:

Videotutorial

Ejercicio (7'27") Sinopsis:

Videotutorial

Suma de términos de una progresión geométrica

Suma de términos de una progresión geométrica

La suma de los n primeros términos de una progresión geométrica es:

$S_n=\frac{a_1.r^n-a_1}{r-1}$

Demostración:

Efectuamos la siguiente resta:

$r \cdot S_n \qquad ~= \qquad \quad a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n +a_n \cdot r$

$-\;$

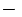
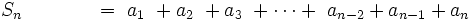
$S_n \ \qquad ~~~~= \ a_1 \ + a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n$

______________________________________________________________________________

$r \cdot S_n- S_n= -a_1 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ~~+a_n \cdot r$

por tanto:

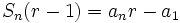
$S_n(r-1)=a_n r-a_1\;$

y despejando

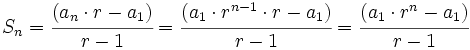
$S_n=\cfrac{(a_n \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^{n-1} \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^n - a_1)}{r-1}$

Suma de los infinitos términos de una progresión geométrica

La suma de todos los términos de una progresión geométrica en la que su razón verifica que 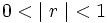$0<\; \mid r \mid \; <1$ se obtiene así:

$S_{\infty}=\frac{a_1}{1-r}$

Demostración:

La siguiente demostración usa el concepto de límite que aún no conoceis. Lo podremos ver con detalle, más adelante en este tema, en un apartado titulado Algunos límites importantes.

Vamos a partir de la fórmula de la suma de los n primeros términos de una progresión geométrica y vamos a hacer que n tienda a infinito.

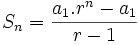
$S_n=\frac{a_1.r^n-a_1}{r-1}$

Como 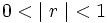$0<\; \mid r \mid \; <1$ , cuando n tiende a infinito, 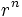$r^n\;$ tiende a 0.

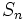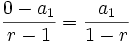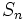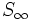Entonces, $S_n\;$ tiende a $\frac{0-a_1}{r-1}=\frac{a_1}{1-r}$ y a ese valor límite de $S_n\;$ lo llamamos $S_{\infty}$ .

Producto de términos de una progresión geométrica

Producto de n términos de una progresión geométrica (7´31") Sinopsis:

Videotutorial

Obtenido de "http://www.maralboran.org/wikipedia/index.php/Plantilla:Progresiones_geom%C3%A9tricas"

 }}
+===Producto de términos de una progresión geométrica===
+{{Video_enlace
+|titulo1=Producto de n términos de una progresión geométrica
+|duracion=7´31"
+|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/06-producto-de-terminos-consecutivos-de-una-sucesion-geometrica#.VCaoBPl_u2E
+|sinopsis=Videotutorial
+}}
+{{p}}

Plantilla:Progresiones geométricas

De Wikipedia

Revisión de 12:10 27 sep 2014

Tabla de contenidos

Progresiones geométricas

Término general de una progresión geométrica

Videotutoriales sobre progesiones geométricas

Suma de términos de una progresión geométrica

Producto de términos de una progresión geométrica

Vistas

Herramientas personales

Menú

Buscar

Herramientas