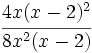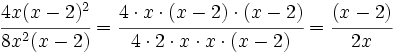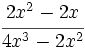Plantilla:Fracciones algebraicas
De Wikipedia
| Revisión de 21:22 27 sep 2014 Coordinador (Discusión | contribuciones) (→Videotutoriales) ← Ir a diferencia anterior |
Revisión de 15:51 7 oct 2014 Coordinador (Discusión | contribuciones) (→Simplificar fracciones algebraicas) Ir a siguiente diferencia → |
||
| Línea 20: | Línea 20: | ||
| |sol= | |sol= | ||
| <math> \cfrac {4x(x-2)^2}{8x^2(x-2)}=\cfrac {4 \cdot x \cdot (x-2) \cdot (x-2)}{4 \cdot 2 \cdot x \cdot x \cdot (x-2)}= \cfrac {(x-2)}{2x}</math> | <math> \cfrac {4x(x-2)^2}{8x^2(x-2)}=\cfrac {4 \cdot x \cdot (x-2) \cdot (x-2)}{4 \cdot 2 \cdot x \cdot x \cdot (x-2)}= \cfrac {(x-2)}{2x}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Simplificación de fracciones algebraicas'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | :Simplifica: | ||
| + | |||
| + | :a) <math>\cfrac{2x^2-2x}{4x^3-2x^2}</math> | ||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=(2x^2-2x)/(4x^3-2x^2)}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 15:51 7 oct 2014
Tabla de contenidos |
Fracción algebraica
Una fracción algebraica es una expresión fraccionaria en la que numerador y denominador son polinomios.
Son fracciones algebraicas:
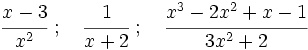
Las fracciones algebraicas tienen un comportamiento similar a las fracciones niuméricas.
Operaciones con fracciones algebraicas
Simplificar fracciones algebraicas
Ejemplos: Simplificar fracciones algebraicas
- Simplifica:
 Actividad: Simplificación de fracciones algebraicas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Suma y resta de fracciones algebraicas
Para sumar y restar procederemos de forma similar que con fracciones de números enteros, reduciendo primero a común denominador.
Ejemplos: Suma y resta de fracciones algebraicas
- Opera:
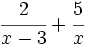
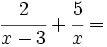El m.c.m. de los denominadores es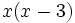 
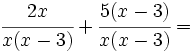Sumamos los numeradores dejando el mismo denominador y simplificamos el numerador:
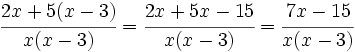
Producto de fracciones algebraicas
Para multiplicar fracciones algebraicas procederemos igual que con fracciones, multiplicando los numeradores y los denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
Ejemplos: Producto de fracciones algebraicas
- Opera:
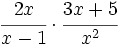
Multiplicamos numeradores y denominadores, pero lo dejamos indicado:
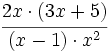
Simplificamos antes de efectuar el producto:
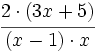
Finalmente, podemos multiplicar, si es preciso:
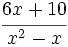
Cociente de fracciones algebraicas
Para dividir fracciones algebraicas procederemos igual que con fracciones, haciendo el producto cruzado de numeradores y denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
Ejemplos: Cociente de fracciones algebraicas
- Opera:
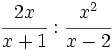
Hacemos el producto cruzado, dejándolo indicado:
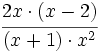
Simplificamos:
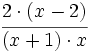
Finalmente, podemos multiplicar, si es preciso:
Videotutoriales
Fracciones algebraicas (4´47") Sinopsis:Si P(x) y Q(x) son polinomios y Q(x) no es el polinomio nulo, llamamos fracción algebraica a toda expresión de la forma P(x)/Q(x). Las fracciones algebraicas A(x)/B(x) y C(x)/D(x) se dicen equivalentes si A(x).D(x) = C(x).D(x), y se escribe A(x)/B(x) = C(x)/D(x). Si el numerador y el denominador de una fracción algebraica se multiplican por un polinomio no nulo, resulta una fracción algebraica equivalente. Si el numerador y el denominador de una fracción algebraica son divisibles por un mismo polinomio, y se dividen, resulta una fracción algebraica equivalente, diciéndose que la primera fracción algebraica se ha "simplificado".
3 ejercicios sobre fracciones algebraicas (5´46") Sinopsis:Videotutorial.
4 ejercicios sobre fracciones algebraicas (6´14") Sinopsis:Videotutorial.
Suma de fracciones algebraicas (6´39") Sinopsis:Videotutorial.
Ejemplo de suma y resta de fracciones algebraicas (6´48") Sinopsis:Videotutorial.
Producto y cociente fracciones algebraicas (3´21") Sinopsis:Videotutorial.
