Plantilla:Discriminante de la ecuación de segundo grado
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 21:27 27 sep 2014 Coordinador (Discusión | contribuciones) (→Discriminante de una ecuación de segundo grado) ← Ir a diferencia anterior |
Revisión de 11:18 29 ago 2016 Coordinador (Discusión | contribuciones) (→Discriminante de una ecuación de segundo grado) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ===Discriminante de una ecuación de segundo grado=== | ===Discriminante de una ecuación de segundo grado=== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Llamamos '''discriminante''' de una ecuación de segundo grado a: | + | Llamamos '''discriminante''' de una ecuación de segundo grado al número: |
| <center><math>\triangle = b^2-4ac</math></center> | <center><math>\triangle = b^2-4ac</math></center> | ||
| - | por tanto: | + | Por tanto: |
| *Si <math>\triangle <0</math> la ecuación no tiene solución. | *Si <math>\triangle <0</math> la ecuación no tiene solución. | ||
| *Si <math>\triangle >0</math> la ecuación tiene dos soluciones. | *Si <math>\triangle >0</math> la ecuación tiene dos soluciones. | ||
Revisión de 11:18 29 ago 2016
Discriminante de una ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado al número:
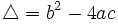
Por tanto:
- Si
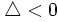la ecuación no tiene solución.
- Si
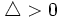la ecuación tiene dos soluciones.
- Si
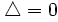la ecuación tiene una solución (doble).
 Actividad Interactiva: Discriminante de una ecuación de segundo grado
Calcula el discriminante de las siguientes ecuaciones de segundo grado.
Actividad:
|
