Distancias en el plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:13 3 oct 2014 Coordinador (Discusión | contribuciones) (→Videotutoriales) ← Ir a diferencia anterior |
Revisión de 17:16 3 oct 2014 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 54: | Línea 54: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Distancia de un punto a una recta''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En esta escena vamos a hallar la distancia del punto <math>P(-5,8)\,</math> a la recta <math>r: \, 2x-6y+7=0</math>. | ||
| - | |actividad= | ||
| - | <center><math>d(P,r)=\cfrac{|Aa+Bb+C|}{\sqrt{A^2+B^2}}=\cfrac{|2 \cdot (-5)-6 \cdot 8+7|}{\sqrt{2^2+6^2}}=\cfrac{51}{\sqrt{40}}=8.06</math> | ||
| - | </center> | ||
| - | |||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_4_2.html | ||
| - | width=520 | ||
| - | height=420 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_4_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | '''Ejercicio:''' | ||
| - | |||
| - | Calcula la distancia del punto <math>P(2,-1)\,</math> a la recta <math>r: \, x-3y+5=0</math> y comprueba el resultado en la escena anterior. | ||
| - | |||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | ==Videotutoriales== | ||
| {{Video_enlace | {{Video_enlace | ||
| |titulo1=Distancia de un punto a una recta | |titulo1=Distancia de un punto a una recta | ||
| Línea 155: | Línea 131: | ||
| }} | }} | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Distancia de un punto a una recta''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1:''' En esta escena vamos a hallar la distancia del punto <math>P(-5,8)\,</math> a la recta <math>r: \, 2x-6y+7=0</math>. | ||
| + | |actividad= | ||
| + | <center><math>d(P,r)=\cfrac{|Aa+Bb+C|}{\sqrt{A^2+B^2}}=\cfrac{|2 \cdot (-5)-6 \cdot 8+7|}{\sqrt{2^2+6^2}}=\cfrac{51}{\sqrt{40}}=8.06</math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_4_2.html | ||
| + | width=520 | ||
| + | height=420 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_4_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | '''Ejercicio:''' | ||
| + | |||
| + | Calcula la distancia del punto <math>P(2,-1)\,</math> a la recta <math>r: \, x-3y+5=0</math> y comprueba el resultado en la escena anterior. | ||
| + | |||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Distancia entre dos rectas== | ||
| {{Video_enlace | {{Video_enlace | ||
| |titulo1=Distancia entre dos rectas paralelas | |titulo1=Distancia entre dos rectas paralelas | ||
| Línea 161: | Línea 162: | ||
| |sinopsis=Videotutorial | |sinopsis=Videotutorial | ||
| }} | }} | ||
| - | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios: ''Distancia entre dos rectas paralelas'' | |titulo=Ejercicios: ''Distancia entre dos rectas paralelas'' | ||
| Línea 172: | Línea 172: | ||
| }} | }} | ||
| }} | }} | ||
| + | ==Bisectrices del ángulo entre dos rectas== | ||
| {{Video_enlace | {{Video_enlace | ||
| - | |titulo1=Bisectrices del ángulo de dos rectas | + | |titulo1=Bisectrices del ángulo entre dos rectas |
| |duracion=5´29" | |duracion=5´29" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/07-bisectrices-del-angulo-de-dos-rectas#.VC7YYxa7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/07-bisectrices-del-angulo-de-dos-rectas#.VC7YYxa7ZV8 | ||
| Línea 180: | Línea 181: | ||
| {{p}} | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| - | |titulo=Ejercicios: ''Bisectrices del ángulo de dos rectas'' | + | |titulo=Ejercicios: ''Bisectrices del ángulo entre dos rectas'' |
| |cuerpo= | |cuerpo= | ||
| {{Video_enlace | {{Video_enlace | ||
Revisión de 17:16 3 oct 2014
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Distancia ente dos puntos
La distancia entre dos puntos 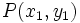 y
y 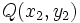 es igual al módulo del vector
es igual al módulo del vector 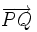 :
:
|
|
|
Actividad Interactiva: Distancia entre dos puntos
Actividad 1: En esta escena vamos a hallar la distancia entre los puntos
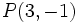 y y 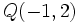 . .Actividad: 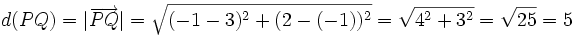
Ejercicio: Calcula la distancia entre los puntos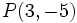 y y 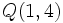 y comprueba el resultado en la escena anterior. y comprueba el resultado en la escena anterior. |
Distancia de un punto a una recta
Proposición
- La distancia del punto
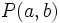 a la recta
a la recta 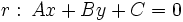 es:
es:
|
|
Videotutorial
|
Ejercicios: Distancia de un punto a una recta Videotutorial Videotutorial Videotutorial Videotutorial Videotutorial Videotutorial Videotutorial Videotutorial Videotutorial Videotutorial Videotutorial |
|
Actividad Interactiva: Distancia de un punto a una recta
Actividad 1: En esta escena vamos a hallar la distancia del punto
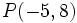 a la recta a la recta 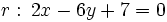 . .Actividad: 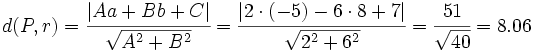
Ejercicio: Calcula la distancia del punto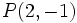 a la recta a la recta 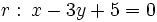 y comprueba el resultado en la escena anterior. y comprueba el resultado en la escena anterior. |
Distancia entre dos rectas
Videotutorial
|
Ejercicios: Distancia entre dos rectas paralelas Videotutorial |
Bisectrices del ángulo entre dos rectas
Videotutorial
|
Ejercicios: Bisectrices del ángulo entre dos rectas Videotutorial Videotutorial |
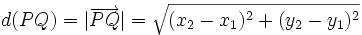
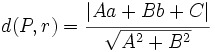
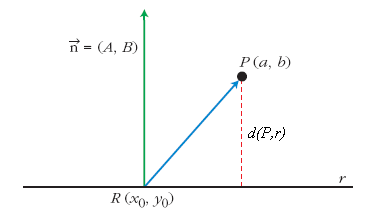
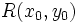 un punto de la recta.
un punto de la recta.
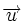
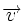
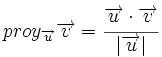
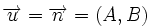
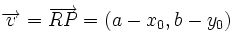
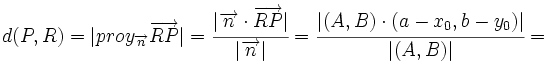
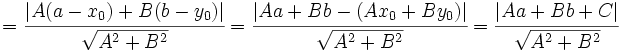
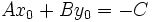 , por ser
, por ser 
