Medida de la correlación (1ºBach)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 17:06 17 oct 2014

Menú:

Enlaces internos	Para repasar o ampliar	Enlaces externos
Indice Descartes Manual Casio		WIRIS Geogebra Calculadoras

Tabla de contenidos

1 Centro de gravedad de una distribución bidimensional
2 Covarianza
3 Coeficiente de correlación
- 3.1 Propiedades del coeficiente de correlación

En el apartado anterior hemos visto de manera intuitiva como puede ser la correlación ente dos variables dependiendo del agrupamiento de los puntos de la nube en torno a una recta. Ahora vamos a ver cómo se puede cuantificar dicha correlación mediante un parámetro que denominaremos coeficiente de correlación.

Consideremos una distribución bidimensional de cuyas variables 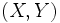$\;(X,Y)$ tenemos 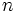$\;n$ valores observados:

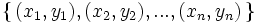
$\{ \,(x_1, y_1), (x_2,y_2),...,(x_n,y_n) \,\}$

Centro de gravedad de una distribución bidimensional

Llamaremos centro de gravedad de la distribución al punto 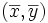$(\overline{x} , \overline{y})$ cuyas coordenadas son las medias de las distribuciones unidimensionales de X e Y:

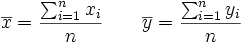
$\overline{x}=\frac{\sum_{i=1}^n x_i}{n} \qquad \overline{y}=\frac{\sum_{i=1}^n y_i}{n}$

Covarianza

Se llama covarianza de la distribución al parámetro:

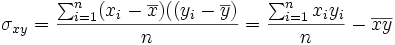
$\sigma_{xy}=\frac{\sum_{i=1}^n (x_i-\overline{x})((y_i-\overline{y})}{n}=\frac{\sum_{i=1}^n x_i y_i}{n}-\overline{x} \overline{y}$

Coeficiente de correlación

Llamaremos coeficiente de correlación entre las dos variables al parámetro:

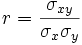
$r= \frac{\sigma_{xy}}{\sigma_x \sigma_y}$

donde $σ x y$ es la covarianza y $σ x,σ y$ son las desviaciones típicas de las distribuciones unidimensionales de X e Y:

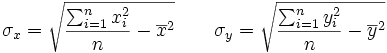
$\sigma_x=\sqrt{\frac{\sum_{i=1}^n x_i^2}{n}-\overline{x}^2} \qquad \sigma_y=\sqrt{\frac{\sum_{i=1}^n y_i^2}{n}-\overline{y}^2}$

Propiedades del coeficiente de correlación

El coeficiente de correlación tiene las siguientes propiedades:

No tiene dimensiones, es decir, no depende de las unidades en las que vengan dadas las variables.
Está comprendido entre -1 y 1: $|r| \le 1$
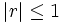
Cuanto más fuerte sea la correlación más próximo a 1 estará 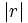$|r| \,$ y cuanto más débil sea la correlación más próximo a 0 estará $|r| \,$ .
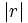Si 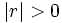$|r|>0 \,$ la correlación será positiva y si 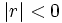$|r|<0 \,$ la correlación será negativa.

Obtenido de "http://maralboran.org/wikipedia/index.php/Medida_de_la_correlaci%C3%B3n_%281%C2%BABach%29"

 En el apartado anterior hemos visto de manera intuitiva como puede ser la correlación ente dos variables dependiendo del agrupamiento de los puntos de la nube en torno a una recta. Ahora vamos a ver cómo se puede cuantificar dicha correlación mediante un parámetro que denominaremos coeficiente de correlación.
-Dada una distribución bidimensional de cuyas variables <math>\;(X,Y)</math> tenemos <math>\;n</math> valores observados:
+Consideremos una distribución bidimensional de cuyas variables <math>\;(X,Y)</math> tenemos <math>\;n</math> valores observados:
 {{p}}
 <center><math>\{ \,(x_1, y_1), (x_2,y_2),...,(x_n,y_n) \,\}</math></center>

Medida de la correlación (1ºBach)

De Wikipedia

Revisión de 17:06 17 oct 2014

Tabla de contenidos

Centro de gravedad de una distribución bidimensional

Covarianza

Coeficiente de correlación

Propiedades del coeficiente de correlación

Vistas

Herramientas personales

Menú

Buscar

Herramientas