Plantilla:Figuras semejantes
De Wikipedia
| Revisión de 12:37 7 ago 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:26 25 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 40: | Línea 40: | ||
| Ya hemos visto antes que escala y razón de semejanza significan lo mismo. El término escala suele utilizarse en planos o mapas. Así, por ejemplo, decimos que un plano está a escala 1:100 si 1 cm en el plano son 100 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es <math>r=\cfrac{1}{100}</math>. | Ya hemos visto antes que escala y razón de semejanza significan lo mismo. El término escala suele utilizarse en planos o mapas. Así, por ejemplo, decimos que un plano está a escala 1:100 si 1 cm en el plano son 100 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es <math>r=\cfrac{1}{100}</math>. | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Escalas''|cuerpo= | + | {{Video_enlace_miguematicas |
| - | {{ai_cuerpo | + | |titulo1=Problema 1 |
| - | |enunciado='''Actividad 1:''' Las dimensiones de una casa. | + | |duracion=3'50" |
| - | |actividad= | + | |url1=https://www.youtube.com/watch?v=6KUXoPtF9lo&list=PLLfTN7MHLxCokf6CRoyuwfardoGhRZgLl&index=14 |
| - | + | |sinopsis=En una fotografía, la imagen de un persona mide 12 cm, ¿qué escala se ha utilizado si la persona mide en realidad 1.80 m?. | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2:''' Problemas. | + | |
| - | |actividad= | + | |
| - | + | ||
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 3:''' Una casa grande. | + | |
| - | |actividad= | + | |
| - | + | ||
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 4:''' Distancia real y distancia en el plano. | + | |
| - | |actividad= | + | |
| - | + | ||
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 5:''' Mapas. | + | |
| - | |actividad= | + | |
| - | + | ||
| }} | }} | ||
| + | {{Video_enlace_miguematicas | ||
| + | |titulo1=Problema 2 | ||
| + | |duracion=2'41" | ||
| + | |url1=https://www.youtube.com/watch?v=Q_O8CExBUEI&list=PLLfTN7MHLxCokf6CRoyuwfardoGhRZgLl&index=15 | ||
| + | |sinopsis=Los planos de un juguete están a escala 1:10. ¿Cuál es la longitud del juguete si en el plano mide 8 cm?. | ||
| }} | }} | ||
Revisión de 17:26 25 jul 2017
Figuras semejantes
De manera intuitiva, dos figuras son semejantes si tienen la misma forma, pero el tamaño es diferente.
Matematicamente, dos figuras semejantes cumplen:
- Los ángulos correspondientes son iguales (misma forma).
- Los segmentos correspondientes son proporcionales.
Se llama razón de semejanza o escala, 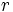 , al cociente entre dos longitudes correspondientes.
, al cociente entre dos longitudes correspondientes.
|
Actividad Interactiva: Figuras semejantes
1. Comprueba las propiedades de dos figuras semejantes.
Actividad: Observa los dos polígonos de la figura. Se dice que son semejantes porque cumplen las dos condiciones antes mencionadas:
En efecto, 1. Los ángulos son iguales ya que los lados correspondientes son paralelos. 2. Para comprobar que los lados son proporcionales usa los segmentos MN y XY que puedes mover libremente. Mide con ellos dos segmentos correspondientes AB y A'B' por ejemplo y calcula la razón de semejanza. Mueve ahora el punto rojo para comprobar el valor de r. |
Escala
Ya hemos visto antes que escala y razón de semejanza significan lo mismo. El término escala suele utilizarse en planos o mapas. Así, por ejemplo, decimos que un plano está a escala 1:100 si 1 cm en el plano son 100 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es 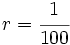 .
.
En una fotografía, la imagen de un persona mide 12 cm, ¿qué escala se ha utilizado si la persona mide en realidad 1.80 m?.
Los planos de un juguete están a escala 1:10. ¿Cuál es la longitud del juguete si en el plano mide 8 cm?.

