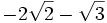Plantilla:Radicales (ampliación)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 19:41 7 ago 2016
Coordinador (Discusión | contribuciones)
(→Extracción e introducción de factores en un radical)
← Ir a diferencia anterior		 Revisión de 19:53 7 ago 2016
Coordinador (Discusión | contribuciones)
(→Suma y resta de radicales con el mismo índice y distinto radicando)
Ir a siguiente diferencia →
Línea 25: Línea 25:
==Suma y resta de radicales con el mismo índice y distinto radicando== ==Suma y resta de radicales con el mismo índice y distinto radicando==
-{{Caja_Amarilla|texto=+ 
-'''Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando:+Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando.
-{{Desplegable|titulo=Ejemplos:{{b}}|contenido=+{{Ejemplo
-Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.+|titulo=Ejemplo: ''Suma y resta de radicales con el mismo índice y distinto radicando''
-<center><iframe>+|enunciado=
-url=http://maralboran.org/web_ma/descartes/3_eso/Radicales/radicales4_1.html+:Suma los siguientes radicales: <math>\sqrt{48}-\sqrt{75}</math>
-width=700+|sol=
-height=210+<math>\sqrt{48}-\sqrt{75}=\sqrt{2^4 \cdot 3}-\sqrt{5^2 \cdot 3}= 2^2\sqrt{3}-5\sqrt{3}=-\sqrt{3}</math>
-name=myframe+
-</iframe></center>+
-<center>[http://maralboran.org/web_ma/descartes/3_eso/Radicales/radicales4_1.html '''Click''' aquí si no se ve bien la escena]</center>+
-}} +
}} }}
{{p}} {{p}}
 +
==Producto y cocientes de radicales de distinto índice== ==Producto y cocientes de radicales de distinto índice==
Para multiplicar o dividir radicales de distinto índice, primero se reducen a índice común y luego se multiplican o dividen los radicandos. Para multiplicar o dividir radicales de distinto índice, primero se reducen a índice común y luego se multiplican o dividen los radicandos.

Revisión de 19:53 7 ago 2016

Tabla de contenidos

Extracción e introducción de factores en un radical

Extracción de factores

Para extaer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto.

ejercicio

Ejemplo: Extracción de factores de un radical

Extrae todo lo que se pueda de este radical: \sqrt[3]{6000}
Solución:
\sqrt[3]{6000}=\sqrt[3]{2^4 \cdot 3 \cdot 5^3}=2 \cdot 5 \sqrt[3]{2 \cdot 3}=10\sqrt[3]{6}

Introducción de factores

Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical.

ejercicio

Ejemplo: Introducción de factores en un radical

Introduce los factores dentro del radical: 10 \sqrt[3]{6}
Solución:
10 \sqrt[3]{6}=\sqrt[3]{6 \cdot 10^3}=\sqrt[3]{6000}

Suma y resta de radicales con el mismo índice y distinto radicando

Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando.

ejercicio

Ejemplo: Suma y resta de radicales con el mismo índice y distinto radicando

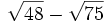
Suma los siguientes radicales: \sqrt{48}-\sqrt{75}
Solución:
\sqrt{48}-\sqrt{75}=\sqrt{2^4 \cdot 3}-\sqrt{5^2 \cdot 3}= 2^2\sqrt{3}-5\sqrt{3}=-\sqrt{3}

Producto y cocientes de radicales de distinto índice

Para multiplicar o dividir radicales de distinto índice, primero se reducen a índice común y luego se multiplican o dividen los radicandos.

ejercicio

Ejemplo: Producto y cocientes de radicales de distinto índice

Reduce a un solo radical \sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}
Solución:

Para reducir los radicales a índice común calculamos el m.c.m de los índices: m.c.m.(3,4,2)=12 y elevamos cada radicando al resultado de dividir el m.c.m. por el índice de cada radical.

\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}=\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}

Luego multiplicamos o dividimos los radicandos, ya que ahora los índices son iguales:

\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}=\sqrt[12]{10^4 \cdot 5^3 : 8^6}

Finalmente simplificamos:

\sqrt[12]{10^4 \cdot 5^3 : 8^6}=\sqrt[12]{2^4 \cdot 5^4 \cdot 5^3 : (2^3)^6}=\sqrt[12]{2^{22} \cdot 5^7}

Racionalización de denominadores

Se llama racionalización al procedimiento por el cual a partir de una fracción con raíces en el denominador obtenemos otra fracción equivalente sin raíces en el denominador

Caso 1: Denominador con raíces cuadradas

Para racionalizar uno radical de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.

ejercicio

Ejemplo: Caso 1: Denominador con raíces cuadradas

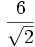
Racionalizar \frac{{6}}{\sqrt{2}}
Solución:

En este caso hay que multiplicar numerador y denominador por 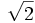\sqrt{2}

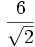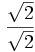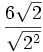
\frac{{6}}{\sqrt{2}} · \frac{\sqrt{2}}{\sqrt{2}} = \frac{{6\sqrt{2}}}{\sqrt{2^2}}


Después se despeja la raíz cuadrada del denominador:

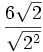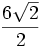
\frac{{6\sqrt{2}}}{\sqrt{2^2}} = \frac{{6\sqrt{2}}}{{2}}


El resultado del ejercicio es éste, aunque se puede simplificar el número entero del numerador entre el del denominador, así:

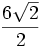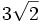
\frac{{6\sqrt{2}}}{{2}} = 3\sqrt{2}

Caso 2: Denominador con otras raíces

En este caso, los exponentes del radicando del radical por el que se deben multiplicar el numerador y denominador de la fracción será la diferencia entre los exponentes actuales y el índice (o múltiplo del indice más cercano) del radical.

ejercicio

Ejemplo: Caso 2: Denominador con otras raíces

Racionalizar \frac{{2}}{\sqrt[5]{a^3b^4}}
Solución:

En este ejemplo, hay que multiplicar por \sqrt[5] {a^2b}, ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz.

Ahora, se procede a multiplicar el numerador y el denominador:

\frac{{2}}{\sqrt[5]{a^3b^4}} · \frac{\sqrt[5] {a^2b} }{\sqrt[5]{a^2b}} = \frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}}

Ahora, se procede al despeje de las raíces, en el ejemplo de índice 5:

\frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}} = \frac{{2\sqrt[5]{a^2b}}}{{ab}}

Caso 3: Denominador con sumas y restas de raíces

Para este último caso, se multiplica y divide por la expresión conjugada del denominador (solo se le cambia el segundo signo de la expresión)

ejercicio

Ejemplo: Caso 3: Denominador con sumas y restas de raíces

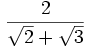
Racionalizar \frac{{2}}{\sqrt{2}+\sqrt{3}}
Solución:

En este caso hay que multiplicar el numerador y el denominador por 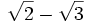{\sqrt{2}-\sqrt{3}}; este resultado es el que da el producto notable de los binomios conjugados.

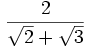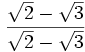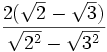
\frac{{2}}{\sqrt{2}+\sqrt{3}} · \frac{{{\sqrt{2}-\sqrt{3}}}}{\sqrt{2}-\sqrt{3}} = \frac{{2({\sqrt{2}-\sqrt{3}}) }}{\sqrt{2^2}-\sqrt{3^2}}

Ahora, se procede al despeje de las raíces cuadradas del denominador:

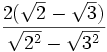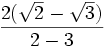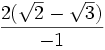\frac{{2({\sqrt{2}-\sqrt{3}}) }}{\sqrt{2^2}-\sqrt{3^2}} = \frac{{2({\sqrt{2}-\sqrt{3}}) }}{{2}-{3}} = \frac{{2({\sqrt{2}-\sqrt{3}}) }}{{-1}} = {-2\sqrt{2}-\sqrt{3}}
Obtenido de "http://www.maralboran.org/wikipedia/index.php/Plantilla:Radicales_%28ampliaci%C3%B3n%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda