Plantilla:Radicales (nivel básico)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:12 8 ago 2016 Coordinador (Discusión | contribuciones) (→Radical) ← Ir a diferencia anterior |
Revisión de 08:16 8 ago 2016 Coordinador (Discusión | contribuciones) (→Suma y resta de radicales con el mismo índice y radicando) Ir a siguiente diferencia → |
||
| Línea 29: | Línea 29: | ||
| ==Suma y resta de radicales con el mismo índice y radicando== | ==Suma y resta de radicales con el mismo índice y radicando== | ||
| - | {{Caja_Amarilla|texto= | + | |
| Para sumar y restar radicales, éstos deben tener el mismo radicando y el mismo índice. | Para sumar y restar radicales, éstos deben tener el mismo radicando y el mismo índice. | ||
| {{p}} | {{p}} | ||
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | {{Ejemplo |
| + | |titulo=Ejemplo: ''Suma y resta de radicales con el mismo índice y radicando'' | ||
| + | |enunciado= | ||
| + | : Efectúa las siguientes sumas y restas de radicales: | ||
| + | #<math>3\sqrt{5}-\sqrt{5}+5\sqrt{5}</math> | ||
| + | #<math>3\sqrt{2}-\sqrt{3}</math> | ||
| + | #<math>3\sqrt[3]{2}+\sqrt{2}</math> | ||
| + | |sol= | ||
| #<math>3\sqrt{5}-\sqrt{5}+5\sqrt{5}=(3-1+5)\sqrt{5}=7\sqrt{5}</math> | #<math>3\sqrt{5}-\sqrt{5}+5\sqrt{5}=(3-1+5)\sqrt{5}=7\sqrt{5}</math> | ||
| #<math>3\sqrt{2}-\sqrt{3}=</math> (No se puede simplificar) | #<math>3\sqrt{2}-\sqrt{3}=</math> (No se puede simplificar) | ||
| #<math>3\sqrt[3]{2}+\sqrt{2}=</math> (No se puede simplificar) | #<math>3\sqrt[3]{2}+\sqrt{2}=</math> (No se puede simplificar) | ||
| }} | }} | ||
| - | }} | + | {{p}} |
Revisión de 08:16 8 ago 2016
Radical
El término radical se usa como sinónimo de raíz
Propiedades de las operaciones con radicales
Propiedades de las operaciones con radicales
- 1.
![\sqrt[np]{a^p}=\sqrt[n]{a}](/wikipedia/images/math/1/9/0/19055926ec943d41884a4e4efb9e3958.png)
- 2.
![\left ( \sqrt[n]{a}\right )^p=\sqrt[n]{a^p}](/wikipedia/images/math/0/8/f/08f48fff6b28e5860652ad48624e9b54.png)
- 3.
![\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}](/wikipedia/images/math/8/8/2/882098878748f7e317a403bacf091e37.png)
- 4.
![\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a \cdot b}](/wikipedia/images/math/7/3/d/73d577cd0a118df1dda404e72e4a922d.png)
- 5.
![\cfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\cfrac{a}{b}}](/wikipedia/images/math/4/8/d/48d4191b86a6079638a33f860884bd8e.png)
Demostración:
Para demostrar estas propiedades basta con expresar el radical como potencia de exponente fraccionario y aplicar sus propiedades.
Ejercicios resueltos: Radicales. Propiedades
- 2. Simplificar: a)
![\sqrt[12]{x^9}](/wikipedia/images/math/9/4/2/942b2336ccb4cf42b2cbd07ed9c75ede.png)
, b) ![\left ( \sqrt[3]{a^2} \right )^6](/wikipedia/images/math/9/a/1/9a1db4aea08869857d67618e54707551.png)
, c) ![\sqrt{\sqrt[3]{a}}](/wikipedia/images/math/4/7/3/473cf1ea29276b3cfe84680bf3548a10.png)
, d) ![\sqrt[3]{\sqrt{a}}](/wikipedia/images/math/0/2/6/026566b7fe0a0a29b75fb2be27d31544.png)
Solución:
- a)
![\sqrt[12]{x^9}=\sqrt[4 \cdot 3]{x^{3 \cdot 3}}=\sqrt[4]{x^{3}}](/wikipedia/images/math/d/1/9/d190b659acadff5f242846e5d6014e10.png)
, usando la propiedad nº 1 de las operaciones con radicales.
- b)
![\left ( \sqrt[3]{a^2} \right )^6=\sqrt[3]{a^{12}}=a^{\frac{12}{3}}=a^4](/wikipedia/images/math/9/4/b/94b477fe13f98eac4d76261cf2c34d2c.png)
, usando la propiedad nº 2 de las operaciones con radicales y transformando el radical en potencia de exponente fraccionario.
- c)
![\sqrt{\sqrt[3]{a}}=\sqrt[2 \cdot 3]{a}=\sqrt[6]{a}](/wikipedia/images/math/9/4/a/94ad123ac81d4cf1d017be5a726de942.png)
, usando la propiedad nº 3 de las operaciones con radicales.
- d)
![\sqrt[3]{\sqrt{a}}=\sqrt[3 \cdot 2]{a}=\sqrt[6]{a}](/wikipedia/images/math/e/0/5/e05d536f330796bbb4297913e3fe710e.png)
, usando la propiedad nº 3 de las operaciones con radicales.
Suma y resta de radicales con el mismo índice y radicando
Para sumar y restar radicales, éstos deben tener el mismo radicando y el mismo índice.
Ejemplo: Suma y resta de radicales con el mismo índice y radicando
- Efectúa las siguientes sumas y restas de radicales:
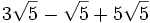
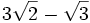
![3\sqrt[3]{2}+\sqrt{2}](/wikipedia/images/math/f/5/5/f554a76b3698de9bd3d86d6600364c25.png)
Solución:
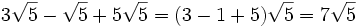
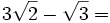(No se puede simplificar)
![3\sqrt[3]{2}+\sqrt{2}=](/wikipedia/images/math/a/6/e/a6edb4be927bfe44dff1ae00ac0eb772.png)
(No se puede simplificar)
