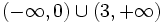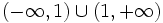Concepto de sucesión (1ºBach)
De Wikipedia
| Revisión de 10:26 12 ago 2016 Coordinador (Discusión | contribuciones) (→Videotutoriales sobre sucesiones) ← Ir a diferencia anterior |
Revisión de 10:45 12 ago 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Sucesión de números reales== | ==Sucesión de números reales== | ||
| + | (pág. 52) | ||
| + | |||
| {{Caja_Amarilla|texto=Una '''sucesión''' de números reales es una función <math>f \;</math>, que a cada número natural <math>n \;</math> le asocia un número real <math>a_n \;</math> | {{Caja_Amarilla|texto=Una '''sucesión''' de números reales es una función <math>f \;</math>, que a cada número natural <math>n \;</math> le asocia un número real <math>a_n \;</math> | ||
| Línea 19: | Línea 21: | ||
| {{p}} | {{p}} | ||
| Se suele identificar a la sucesión con sus términos. Así, muchas veces, hablaremos de la sucesión de términos <math>\{ a_1,\ a_2,\ a_3,\ \cdots \}</math> en lugar de la sucesión <math>f \;</math>. | Se suele identificar a la sucesión con sus términos. Así, muchas veces, hablaremos de la sucesión de términos <math>\{ a_1,\ a_2,\ a_3,\ \cdots \}</math> en lugar de la sucesión <math>f \;</math>. | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejercicios resueltos: ''Concepto de sucesión'' | ||
| + | |enunciado= :Descubre el criterio por el que se forman las sucesiones siguientes y añade dos términos más a cada una: | ||
| + | ::a) 1, 4, 9, 16, 25, 36, ... | ||
| + | ::b) 2, 4, 8, 16, 32, 64, ... | ||
| + | ::c) 1, -3, 9, -27, 81, ... | ||
| + | ::d) 2, 4, 6, 10, 16, 26, ... | ||
| + | ::e) 110, 90, 70, 50, 30, ... | ||
| + | ::f) 1, -4, 9, -16, 25, -36, ... | ||
| + | |sol= | ||
| + | :a) Cada término es el cuadrado del lugar que ocupa. | ||
| + | ::<math>a_7=49,\ a_8=64</math> | ||
| + | |||
| + | :b) Cada término, a partir del segundo, se obtiene multiplicando por 2 el anterior. | ||
| + | ::<math>b_7=128,\ b_8=256</math> | ||
| + | |||
| + | :c) Cada término, a partir del segundo, se obtiene multiplicando por -3 el anterior. | ||
| + | ::<math>c_7=-243,\ c_8=729</math> | ||
| + | |||
| + | :d) Cada término, a partir del tercero, se obtiene sumando los dos anteriores. | ||
| + | ::<math>d_7=42,\ d_8=68</math> | ||
| + | |||
| + | :e) Cada término, a partir del segundo, se obtiene restándo 20 al anterior. | ||
| + | ::<math>e_6=10,\ e_7=-10</math> | ||
| + | |||
| + | :f) Los términos pares, a partir del segundo, se obtienen sumando 2 al anterior. | ||
| + | ::<math>f_8=38 \;</math> | ||
| + | ::y los términos impares, a partir del tercero, se obtienen multiplicando por 2 el anterior. | ||
| + | ::<math>f_9=76 \;</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Ejercicios== | ||
| + | (pág. 52) | ||
| + | |||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Intervalos y semirectas'' | ||
| + | |cuerpo= | ||
| + | [[Imagen:yellow_star.png|12px]]'''3.''' Representa los siguientes conjuntos: | ||
| + | :a) <math>\left ( -3, -1 \right )</math> | ||
| + | :b) <math>\left [ 4, +\infty \right )</math> | ||
| + | :c) <math>\left ( 3, 9 \right ]</math> | ||
| + | :d) <math>\left ( -\infty, 0 \right )</math> | ||
| + | |||
| + | [[Imagen:yellow_star.png|12px]]'''4.''' Representa los siguientes conjuntos: | ||
| + | :a) <math>\left \{ x \in \mathbb{R} \ / -2 \le x<5 \right \}</math> | ||
| + | :b) <math>\left [ -2, 5 \right ) \cup \left ( 5, 7 \right ]</math> | ||
| + | :c) <math>\left (-\infty , 0 \right ) \cup \left (3, +\infty \right )</math> | ||
| + | :d) <math>\left (-\infty , 1 \right ) \cup \left (1, +\infty \right )</math> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| ===La sucesión de Fibonacci y el número áureo=== | ===La sucesión de Fibonacci y el número áureo=== | ||
Revisión de 10:45 12 ago 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Sucesión de números reales
(pág. 52)
Una sucesión de números reales es una función 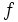 , que a cada número natural
, que a cada número natural 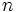 le asocia un número real
le asocia un número real 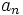
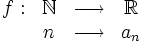
Esto genera el conjunto ordenado
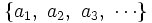
que se llaman los términos de la sucesión.
Se suele identificar a la sucesión con sus términos. Así, muchas veces, hablaremos de la sucesión de términos 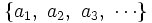 en lugar de la sucesión
en lugar de la sucesión 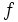 .
.
Ejercicios resueltos: Concepto de sucesión
- Descubre el criterio por el que se forman las sucesiones siguientes y añade dos términos más a cada una:
- a) 1, 4, 9, 16, 25, 36, ...
- b) 2, 4, 8, 16, 32, 64, ...
- c) 1, -3, 9, -27, 81, ...
- d) 2, 4, 6, 10, 16, 26, ...
- e) 110, 90, 70, 50, 30, ...
- f) 1, -4, 9, -16, 25, -36, ...
- a) Cada término es el cuadrado del lugar que ocupa.
- b) Cada término, a partir del segundo, se obtiene multiplicando por 2 el anterior.
- c) Cada término, a partir del segundo, se obtiene multiplicando por -3 el anterior.
- d) Cada término, a partir del tercero, se obtiene sumando los dos anteriores.
- e) Cada término, a partir del segundo, se obtiene restándo 20 al anterior.
- f) Los términos pares, a partir del segundo, se obtienen sumando 2 al anterior.
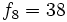
- y los términos impares, a partir del tercero, se obtienen multiplicando por 2 el anterior.
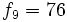
Ejercicios
(pág. 52)
|
Ejercicios propuestos: Intervalos y semirectas |
La sucesión de Fibonacci y el número áureo
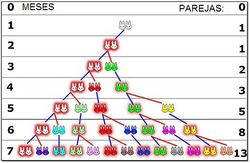
Ejemplo: La sucesión de Fibonacci y el número áureo
- El siguiente problema fue propuesto por Fibonacci, matemático italiano del siglo XIII:
- "Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?"
- a) Escribe la sucesión cuyos términos son lás parejas de conejos que hay cada més. Esta recibe el nombre de sucesión de Fibonacci.
- b) Ahora vas a construir la sucesión que se obtiene al dividir cada término entre el anterior. Esa sucesión verás que se aproxima al número áureo (
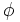 ):
):
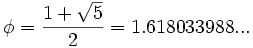
a) Sucesión de Fibonacci:
- Valor inicial: 1 pareja
- Mes 1: 1 pareja (hasta el segundo mes no se reproduce la primera)
- Mes 2: 2 parejas (primera vez que se reproduce)
- Mes 3: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el próximo mes)
- Mes 4: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no)
- Mes 5: 8 parejas (se reproducen las 3 primeras parejas, las otras dos no)
- Mes 6: 13 parejas (se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no)
Así se obtiene una sucesión en la que cada término se obtiene a partir de la suma de los dos anteriores:
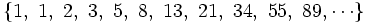
b) Sucesión del número áureo:
Dividiendo cada término entre el anterior, tenemos la sucesión:
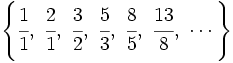
que expresada con decimales vemos que se aproxima al número áureo:
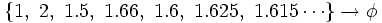
Término general de una sucesión
(pág. 53)
Se llama término general de una sucesión, y se simboliza por 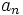 , al término que representa a uno cualquiera de ella. La sucesión correspondiente se representa de forma abreviada por
, al término que representa a uno cualquiera de ella. La sucesión correspondiente se representa de forma abreviada por 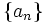
- Hay veces que el término general se puede expresar mediante una fórmula:
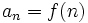 . Dándole a n un valor, se obtiene el término correspondiente.
. Dándole a n un valor, se obtiene el término correspondiente.
- Otras veces, cada término de la sucesión se obtiene a partir de operaciones con otros términos anteriores. A estas sucesiones se les llama recurrentes. En ellas, para hallar un término, tenemos que hallar todos los anteriores.
Ejercicios resueltos: Término general de una sucesión
- Halla el término general de las siguientes sucesiones:
- a) 1, 4, 9, 16, 25, 36, ...
- b) 2, 4, 8, 16, 32, 64, ...
- c) 1, -3, 9, -27, 81, ...
- d) 2, 4, 6, 10, 16, 26, ...
- e) 110, 90, 70, 50, 30, ...
- f) 1, -4, 9, -16, 25, -36, ...
- a)
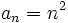
- b)
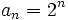
- c)
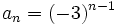
- d) Es recurrente. La ley de recurrencia es
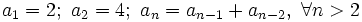
- e)
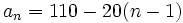
- f)
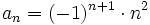
Videotutoriales sobre sucesiones
El concepto de función o aplicación ente dos conjuntos es necesario para la definición de sucesión.
- Definición de sucesión de números reales como aplicación entre el conjunto de los números naturales y el de los números reales.
- Término general de una sucesión.
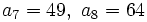
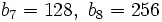
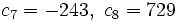
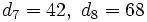
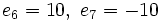
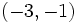
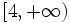
![\left ( 3, 9 \right ]](/wikipedia/images/math/3/b/4/3b4e6238e73719545001ae38eb4d10f6.png)
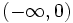
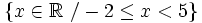
![\left [ -2, 5 \right ) \cup \left ( 5, 7 \right ]](/wikipedia/images/math/e/6/6/e663923d792f5e24c5482f7a6c34c329.png)