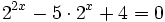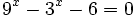Plantilla:Ecuaciones exponenciales

De Wikipedia

(Diferencia entre revisiones)
Revisión de 08:47 30 ago 2016
Coordinador (Discusión | contribuciones)

← Ir a diferencia anterior		 Revisión de 09:08 30 ago 2016
Coordinador (Discusión | contribuciones)

Ir a siguiente diferencia →
Línea 49: Línea 49:
-'''''Soluciones:''''' <math>x_1=2 , \ x_2=3;</math>+:'''''Soluciones:''''' <math>x_1=2 , \ x_2=3;</math>
---- ----
'''c)''' '''c)'''
Línea 60: Línea 60:
:Aplicando la propiedad del logaritmo de una potencia: :Aplicando la propiedad del logaritmo de una potencia:
-<center><math>(1-x^2) log \ 3= log \ 2 \rightarrow 1-x^2= \cfrac{log \ 2}{log \ 3}</math></center>+<center><math>(1-x^2) \ log \ 3= log \ 2 </math></center>
:Y resolvemos la ecuación de segundo grado incompleta: :Y resolvemos la ecuación de segundo grado incompleta:
-<center><math>x^2=1-\cfrac{log \ 2}{log \ 3} \rightarrow \ x=\pm \sqrt{1-\cfrac{log \ 2}{log \ 3}} \approx \pm 0.6075 </math></center>+<center><math>1-x^2= \cfrac{log \ 2}{log \ 3} \rightarrow x^2=1-\cfrac{log \ 2}{log \ 3} \rightarrow \ x=\pm \sqrt{1-\cfrac{log \ 2}{log \ 3}} \approx \pm 0.6075 </math></center>
{{b}} {{b}}
{{p}} {{p}}
Línea 70: Línea 70:
---- ----
 +'''d)'''
 +<center><math>2^x+2^{x+1}=12\;</math></center>
 +{{p}}
 +:Haciendo el cambio de variable:
 +
 +<center><math>2^x=y \;</math></center>
 +
 +:tenemos que:
 +<center><math>2^{x+1}=2^x \cdot 2^1 = 2y \;</math></center>
 +
 +:Y la ecuación de partida queda:
 +{{p}}
 +<center><math>y+2y=12\;</math></center>
 +
 +:Resolvemos la ecuación de primer grado:
 +
 +<center><math>3y=12 \rightarrow y = 4 \;</math></center>
 +
 +:Y deshacemos el cambio de variable:
 +
 +<center><math>y=4 \rightarrow 2^x=4 \rightarrow x = 2 \;</math></center>
 +{{b}}
 +{{p}}
 +:'''''Solución:''''' <math>x=2 \;</math>
 +
}} }}
{{p}} {{p}}
Línea 78: Línea 103:
|enunciado= |enunciado=
-Resuelve las siguientes ecuaciones:+:Resuelve las siguientes ecuaciones:
 + 
 +::a) <math>3^x=\sqrt[3]{9} \;</math>
 + 
 +::b) <math>2^{2x}-5\cdot 2^x+4=0 \;</math>
-:<math>a)\ 3^x=\sqrt[3]{9} \quad b)\ 2^{2x}-5\cdot 2^x+4=0 \quad c)\ 9^x-3^x-6=0 </math>+::c) <math>9^x-3^x-6=0 \;</math>
{{p}} {{p}}
|sol= |sol=
Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
-:a) {{consulta|texto=solve 3^x=3root (9) over the reals}} {{b4}} b) {{consulta|texto=solve 2^(2x)-5*2^x+4=0 over the reals}} {{b4}} c) {{consulta|texto=solve 9^x-3^x-6=0 over the reals}}+:a) {{consulta|texto=solve 3^x=3root (9) over the reals}}
 +:b) {{consulta|texto=solve 2^(2x)-5*2^x+4=0 over the reals}}
 +:c) {{consulta|texto=solve 9^x-3^x-6=0 over the reals}}
{{widget generico}} {{widget generico}}

Revisión de 09:08 30 ago 2016

Las ecuaciones exponenciales son aquellas en las que la incógnita aparece como exponente.

ejercicio

Ejercicios resueltos: Ecuación exponencial

Resuelve las siguientes ecuaciónes:

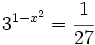
a) 3^{1-x^2}=\cfrac{1}{27}\;
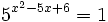
b) 5^{x^2-5x+6}=1 \;
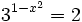
c) 3^{1-x^2}=2\;
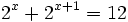
d) 2^x+2^{x+1}=12\;
Solución:

a)

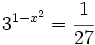
3^{1-x^2}=\cfrac{1}{27}\;
Expresamos el segundo miembro como potencia de 2:
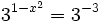
3^{1-x^2}=3^{-3}
Como 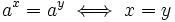a^x = a^y \iff x=y, los exponentes deben ser iguales:
1-x^2=-3\;
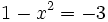
Y resolvemos la ecuación de segundo grado incompleta:
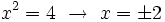
x^2=4 \ \rightarrow \ x=\pm 2

 

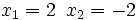
Soluciones: x_1=2 \, \ x_2=-2

b)

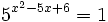
5^{x^2-5x+6}=1 \;
Expresamos el segundo miembro como potencia de 5:
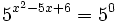
5^{x^2-5x+6}=5^0 \;
Como 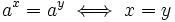a^x = a^y \iff x=y, los exponentes deben ser iguales:
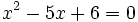
x^2-5x+6=0 \;
Resolvemos la ecuación de segundo grado:
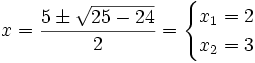
x = \frac{5 \pm \sqrt{25-24}}{2}= \begin{cases} x_1=2 \\ x_2=3 \end{cases}


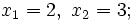
Soluciones: x_1=2 , \ x_2=3;

c)

3^{1-x^2}=2\;

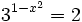
Como el segundo miembro no podemos expresarlo como potencia de base 3, tomaremos logaritmos en ambos lados de la ecuación:

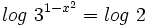
log \ 3^{1-x^2}= log \ 2
Aplicando la propiedad del logaritmo de una potencia:
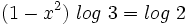
(1-x^2) \ log \ 3= log \ 2
Y resolvemos la ecuación de segundo grado incompleta:
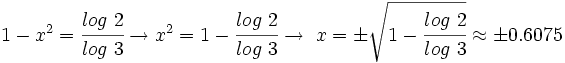
1-x^2= \cfrac{log \ 2}{log \ 3} \rightarrow x^2=1-\cfrac{log \ 2}{log \ 3} \rightarrow \ x=\pm \sqrt{1-\cfrac{log \ 2}{log \ 3}} \approx \pm 0.6075

 

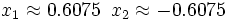
Soluciones: x_1 \approx 0.6075 \, \ x_2 \approx -0.6075

d)

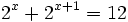
2^x+2^{x+1}=12\;

Haciendo el cambio de variable:
2^x=y \;
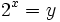
tenemos que:
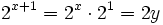
2^{x+1}=2^x \cdot 2^1 = 2y \;
Y la ecuación de partida queda:

y+2y=12\;
Resolvemos la ecuación de primer grado:
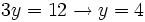
3y=12 \rightarrow y = 4 \;
Y deshacemos el cambio de variable:
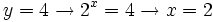
y=4 \rightarrow 2^x=4 \rightarrow x = 2 \;

 

Solución: x=2 \;

wolfram

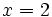
Actividad: Ecuaciones exponenciales

Resuelve las siguientes ecuaciones:
a) 3^x=\sqrt[3]{9} \;
b) 2^{2x}-5\cdot 2^x+4=0 \;
c) 9^x-3^x-6=0 \;

Solución:
Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
a) solve 3^x=3root (9) over the reals
b) solve 2^(2x)-5*2^x+4=0 over the reals
c) solve 9^x-3^x-6=0 over the reals

Obtenido de "http://www.maralboran.org/wikipedia/index.php/Plantilla:Ecuaciones_exponenciales"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda