Plantilla:Def numeros primos y compuestos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:13 6 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:04 12 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 2: | Línea 2: | ||
| celda1= | celda1= | ||
| {{p}}{{Caja_Amarilla|texto= | {{p}}{{Caja_Amarilla|texto= | ||
| - | Un número natural es '''compuesto''' si se puede expresar como producto de otros dos números naturales distintos de él y la unidad. En caso contrario es un número '''primo'''.}} | + | *Un número '''primo''' es un número natural, mayor que 1, que sólo tiene dos divisores: él mismo y el 1. |
| + | *Un número es '''compuesto''' si tiene más de dos divisores.}} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Propiedad|enunciado=:Un número compuesto puede ponerse como producto de dos números distintos de él y la unidad.}} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos|contenido= | {{Ejemplo_simple|titulo=Ejemplos|contenido= | ||
| *15 es compuesto porque 15 = 3·5. | *15 es compuesto porque 15 = 3·5. | ||
| *Los números 2, 3, 5, 7, 11, 13 son primos.}} | *Los números 2, 3, 5, 7, 11, 13 son primos.}} | ||
| - | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Propiedad|enunciado=:Un número primo sólo tiene por divisores a la unidad y a él mismo.}} | ||
| |celda2= | |celda2= | ||
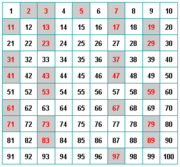
| [[Imagen:tabla_primos.png|center|thumb|Números primos menores que 100]] | [[Imagen:tabla_primos.png|center|thumb|Números primos menores que 100]] | ||
| }} | }} | ||
Revisión de 07:04 12 sep 2016
Propiedad
|