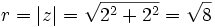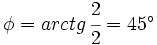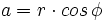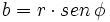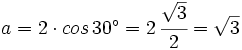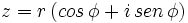Números complejos: Forma polar (1ºBach)
De Wikipedia
| Revisión de 15:57 4 oct 2016 Coordinador (Discusión | contribuciones) (→Forma trigonométrica de un número complejo) ← Ir a diferencia anterior |
Revisión de 15:57 4 oct 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| + | __TOC__ | ||
| {{p}} | {{p}} | ||
| + | (Pág. 152) | ||
| ==Forma polar de un número complejo== | ==Forma polar de un número complejo== | ||
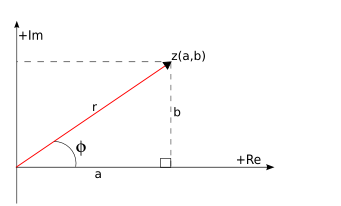
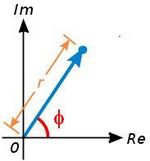
| {{Tabla75|celda2=[[Imagen:complejopolar.jpg|thumb|150px|Fig. 1: Un número complejo queda determinado por su módulo y su argumento.]]|celda1= | {{Tabla75|celda2=[[Imagen:complejopolar.jpg|thumb|150px|Fig. 1: Un número complejo queda determinado por su módulo y su argumento.]]|celda1= | ||
| Línea 84: | Línea 86: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | (Pág. 153) | ||
| ==Paso de forma polar a binómica== | ==Paso de forma polar a binómica== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
Revisión de 15:57 4 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 152)
Forma polar de un número complejo
Dado un número complejo
La forma polar del número complejo (El cero, al no tener argumento, no se puede poner en forma polar) |
Paso de forma binómica a polar
Proposición
Dado un número complejo 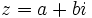 su forma polar
su forma polar 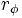 se obtiene de la siguiente manera:
se obtiene de la siguiente manera:
| 
|
Ejemplo: Paso de forma binómica a polar
Pasa a forma polar:
- a)
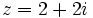
- b)
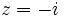
- c)
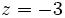
a) 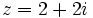
Calculamos el módulo:
Calculamos el argumento:
Solución: 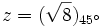
b) 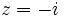
Solución: 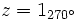
c) 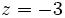
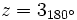
Pasa los siguientes números complejos a forma polar y comprueba tus resultados en la escena:
- a)
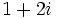 b)
b)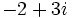 c)
c) 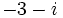 d)
d)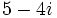
- a)
En esta escena puedes pasar un complejo de forma binómica a polar. Puedes variar los valores de a y b o mover el afijo con el ratón.
(Pág. 153)
Paso de forma polar a binómica
Dado un número complejo 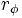 , su forma binómica
, su forma binómica 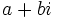 se obtiene de la siguiente manera:
se obtiene de la siguiente manera:
Ejemplo: Paso de forma polar a binómica
Pasa a forma binómica el número complejo 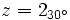
Calculamos la parte real:
Calculamos su parte imaginaria:
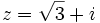
Pasa los siguientes números complejos a forma binómica y comprueba tus resultados en esta escena:
- a)
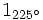 b)
b)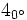 c)
c) 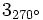 d)
d)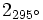 e)
e)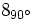 f)
f)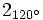
- a)
En esta escena puedes pasar un complejo de forma polar a binómica. Puedes variar los valores del módulo y del argumento.
Forma trigonométrica de un número complejo
Según lo visto en el apartado anterior:

Se llama forma trigonométrica de un número complejo, a la expresión
|
|
Ejemplo: Forma trigonométrica de un complejo
Pasa a forma trigonométrica el número complejo 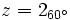
Tan sólo hay que aplicar la fórmula:
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Ejercicios propuestos
|
Ejercicios propuestos: Definición de número complejo |
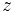 es la longitud del vector que lo representa, es decir, la distancia entre el afijo
es la longitud del vector que lo representa, es decir, la distancia entre el afijo 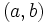 y el origen
y el origen 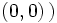 . Se designa por
. Se designa por 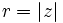 .
.
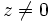 ), es el ángulo que forma el vector con el eje X . Se designa por
), es el ángulo que forma el vector con el eje X . Se designa por 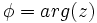 . De los infinitos argumentos de un número complejo, al comprendido entre 0º y 360º se le llama argumento principal.
. De los infinitos argumentos de un número complejo, al comprendido entre 0º y 360º se le llama argumento principal.
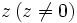 , se designa
, se designa 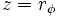 , entonces:
, entonces:
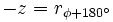
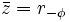
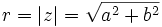
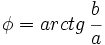
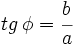 .
.