Tendencias de una función (3ºESO Académicas)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:35 4 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:44 4 nov 2016 Coordinador (Discusión | contribuciones) (→Tendencia de una función) Ir a siguiente diferencia → |
||
| Línea 24: | Línea 24: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| + | {{p}} | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicio: ''Tendencia de una función'' | ||
| + | |cuerpo= | ||
| + | |||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | '''1. '''Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%. | ||
| + | :a) Haz una tabla que exprese el precio del coche durante los próximos años. | ||
| + | :b) Representa gráficamente los resultados del apartado a). | ||
| + | :c) Encuentra una fórmula que exprese esta función. | ||
| + | :d) ¿Cómo es la variable independiente: continua o discreta? | ||
| + | :e) ¿Cuál es el dominio de esta función?. ¿Y su imagen? | ||
| + | :f) ¿Cual es la tendencia de esta función segun pasan los años? | ||
| + | :g) Describe el crecimiento e indica si tiene máximos o mínimos. | ||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | {{p}} | ||
| + | :a) Tabla de valores:{{p}} | ||
| + | <center> | ||
| + | <table border=1> | ||
| + | <tr> | ||
| + | <td>{{b}}x{{b}}</td> | ||
| + | <td>0</td> | ||
| + | <td>1</td> | ||
| + | <td>2</td> | ||
| + | <td>3</td> | ||
| + | <td>4</td> | ||
| + | <td>5</td> | ||
| + | <td>6</td> | ||
| + | <td>7</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td>{{b}}y{{b}}</td> | ||
| + | <td>12.000</td> | ||
| + | <td>9.600</td> | ||
| + | <td>7.680</td> | ||
| + | <td>6.144</td> | ||
| + | <td>4.915,2</td> | ||
| + | <td>3.932,2</td> | ||
| + | <td>3.145,7</td> | ||
| + | <td>2.516,6</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | </center> | ||
| + | {{p}} | ||
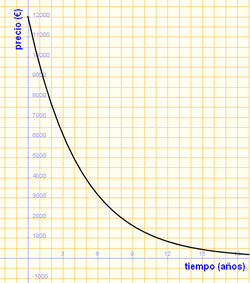
| + | :b) Representación gráfica: | ||
| + | {{p}} | ||
| + | [[Imagen:devalua.png|center|250px]]<br> | ||
| + | :c) Continua. | ||
| + | :d) <math>y=12000 \cdot 0,8^x \quad</math> (€) | ||
| + | :e) <math>D=\mathbb{R}^+</math>; <math>Im=[12.000, \ 0)</math>. | ||
| + | :f) La función tiende a 0 a medida que transcurre el tiempo. | ||
| + | :g) Es decreciente en todo su dominio. Tiene un máximo en <math>x=0</math> y no tiene mínimos. | ||
| + | :h) No es periódica. | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Tendencias|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Tendencias'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | |||
| + | :a) Averigua la tendencia de la función <math>f(x)=\cfrac{1}{x}\;</math>. cuando <math>x\;</math> se hace infinitamente grande. | ||
| + | :b) Observa lo que ocurre en el apartado anterior dibujando la función desde x=0 a x=100000. | ||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=limit x to +oo 1/x}} | ||
| + | :b) {{consulta|texto=plot 1/x {x,0,100000}}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| ==Periodicidad== | ==Periodicidad== | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
Revisión de 19:44 4 nov 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 150)
Tendencia de una función
Decimos que una función 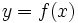 tiende a un valor
tiende a un valor 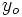 (al aumentar la variable
(al aumentar la variable  indefinidamente) si los valores de la variable dependiente
indefinidamente) si los valores de la variable dependiente 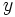 se acercan a
se acercan a 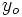 cuando la variable
cuando la variable  toma valores suficientemente grandes.
toma valores suficientemente grandes.
Simbólicamente:
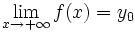
En esta escena podrás estudiar la tendencia de una función que relaciona la temperatura de un recipiente de agua que se va enfriando y el tiempo que ha transcurrido.
|
Ejercicio: Tendencia de una función 1. Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%.
Solución:
|
|
Actividad: Tendencias
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Periodicidad
Ejercicios propuestos
|
Ejercicios propuestos: Las funciones y sus gráficas |
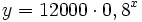 (€)
(€)
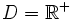 ;
; 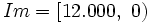 .
.
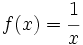 . cuando
. cuando 
