Tendencias de una función (3ºESO Académicas)
De Wikipedia
| Revisión de 20:02 4 nov 2016 Coordinador (Discusión | contribuciones) (→Periodicidad) ← Ir a diferencia anterior |
Revisión de 08:59 12 jul 2017 Coordinador (Discusión | contribuciones) (→Tendencia de una función) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| {{Caja Amarilla | {{Caja Amarilla | ||
| |texto= | |texto= | ||
| - | Decimos que una función <math>y=f(x)\;</math> '''tiende''' a un valor <math>y_o\;</math> (al aumentar la variable <math>x\;</math> indefinidamente) si los valores de la variable dependiente <math>y\;</math> se acercan a <math>y_o\;</math> cuando la variable <math>x\;</math> toma valores suficientemente grandes. | + | Decimos que una función <math>y=f(x)\;</math> '''tiende''' a un valor <math>y_o\;</math> cuando aumenta la variable <math>x\;</math> indefinidamente, si los valores de la variable dependiente <math>y\;</math> se acercan a <math>y_o\;</math> cuando la variable <math>x\;</math> toma valores suficientemente grandes. |
| Simbólicamente: | Simbólicamente: | ||
Revisión de 08:59 12 jul 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 150)
Tendencia de una función
Decimos que una función 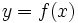 tiende a un valor
tiende a un valor 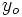 cuando aumenta la variable
cuando aumenta la variable  indefinidamente, si los valores de la variable dependiente
indefinidamente, si los valores de la variable dependiente 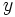 se acercan a
se acercan a 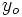 cuando la variable
cuando la variable  toma valores suficientemente grandes.
toma valores suficientemente grandes.
Simbólicamente:
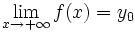
En esta escena podrás estudiar la tendencia de una función que relaciona la temperatura de un recipiente de agua que se va enfriando y el tiempo que ha transcurrido.
|
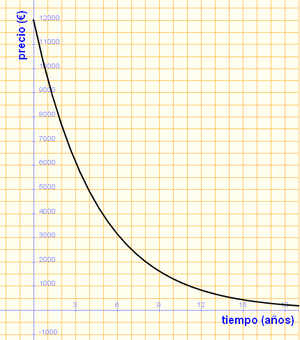
Ejercicio resuelto: Tendencia de una función 1. Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%.
Solución:
|
|
Actividad: Tendencias
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Periodicidad
Una función es periódica si su gráfica se va repitiendo a intervalos. Al menor valor posible, T, de la longitud de dicho intervalo, se le llama periodo. Se cumple: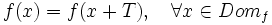 |
Actividades con las que aprenderás a determinar si una función es periódica y a hallar su período a partir de su gráfica.
|
Actividad: Funciones periódicas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Estudio de la periodicidad de una función dada por una gráfica.
Ejercicios propuestos
|
Ejercicios propuestos: Las funciones y sus gráficas |
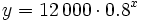 (€)
(€)
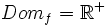 ;
; ![Im_f=(0,12\,000]](/wikipedia/images/math/7/c/a/7cafbf61f55a21ad66bd23e5f5d1fc6b.png) .
.
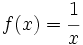 cuando
cuando