Plantilla:Derivada (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:24 28 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:29 28 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 44: | Línea 44: | ||
| |duracion=5'16" | |duracion=5'16" | ||
| |sinopsis=Cálculo de la derivada de <math>y=\frac{x^2}{x-1} \;</math> en el punto <math>x=2\;</math>. | |sinopsis=Cálculo de la derivada de <math>y=\frac{x^2}{x-1} \;</math> en el punto <math>x=2\;</math>. | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0405_04.html | + | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/18-derivabilidad-de-funciones/0504-ejercicio-7#.WGOTckZ9Vko |
| }} | }} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| - | |titulo1=5. Funciones que se nos escapan de las manos. | + | |titulo1=5. Función a trozos |
| - | |duracion=11'50" | + | |
| - | |sinopsis=Algunos ejemplos de derivadas en un punto que no podemos calcular con los conocimientos que tenemos hasta ahora. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0405_05.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=6. Función a trozos | + | |
| |duracion=16'37" | |duracion=16'37" | ||
| |sinopsis=Cálculo de la derivada en un punto de una función a trozos. | |sinopsis=Cálculo de la derivada en un punto de una función a trozos. | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/18-derivabilidad-de-funciones/0505-tres-ejercicios-con-funciones-definidas-a-trozos#.WGOS1EZ9Vko | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/18-derivabilidad-de-funciones/0505-tres-ejercicios-con-funciones-definidas-a-trozos#.WGOS1EZ9Vko | ||
| - | }} | + | }}}} |
| - | {{Video_enlace2 | + | |
| - | |titulo1=7. Función con derivada infinita | + | |
| - | |duracion=14'56" | + | |
| - | |sinopsis=:Cálculo de la derivada de una función en un punto de tangente vertical (derivada infinita). | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0405_07.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=8. Funciones valor absoluto | + | |
| - | |duracion=8'31" | + | |
| - | |sinopsis=:Cálculo de la derivada en un punto de funciones valor absoluto. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0405_08.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=9. Funciones a trozos | + | |
| - | |duracion=5'20" | + | |
| - | |sinopsis=:Cálculo de la derivada en un punto de funciones a trozos. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0405_09.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=10. Funciones a trozos | + | |
| - | |duracion=8'01" | + | |
| - | |sinopsis=:Cálculo de la derivada en un punto de funciones a trozos. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0405_10.html | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=11. Derivada en un punto genérico | + | |
| - | |duracion=13'43" | + | |
| - | |sinopsis=:Cálculo de la derivada en un punto genérico. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0405_11.html | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{ejemplo2 | + | |
| - | |titulo=Ejemplos: ''Cálculo de la derivada de una función en un punto'' | + | |
| - | |enunciado= | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=1. Ejemplos | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0213_01.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=2. Ejemplos | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0213_02.html | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
Revisión de 10:29 28 dic 2016
Aproximación intuitiva al concepto de función derivable.
Apróximación al concepto de derivada apoyándonos en la existencia o no de la recta tangente en un punto.
Definición rigurosa de derivada de una función en un punto.
Ejemplos: Derivada de una función en un punto
Cálculo de la derivada de una función en un punto recurriendo a la definición de derivada, es decir, usando límites.
Cálculo de derivada de 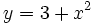 en el punto
en el punto 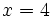 .
.
Cálculo de la derivada de 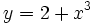 en el punto
en el punto 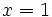 .
.
Cálculo de la derivada de 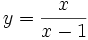 en el punto
en el punto 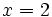 .
.
Cálculo de la derivada de 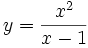 en el punto
en el punto 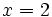 .
.
Cálculo de la derivada en un punto de una función a trozos.

