Ecuaciones (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:27 7 feb 2017 Coordinador (Discusión | contribuciones) (→Resolver una ecuación) ← Ir a diferencia anterior |
Revisión de 12:32 7 feb 2017 Coordinador (Discusión | contribuciones) (→Elementos de una ecuación) Ir a siguiente diferencia → |
||
| Línea 20: | Línea 20: | ||
| ==Elementos de una ecuación== | ==Elementos de una ecuación== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | Una ecuación es una igualdad entre dos expresiones algebraicas. | ||
| + | *A cada una de las dos expresiones algebraicas separadas por el signo igual se les llama '''miembros''' de la ecuación: el '''primer miembro''' es el que está a la izquierda de la igualdad y el '''segundo miembro''' el que está a la derecha. | ||
| + | *Cada uno de los sumandos que forman cada miembro de la ecuación se llaman '''términos''' de la ecuación. | ||
| + | *Las '''incógnitas''' son las letras que aparecen en los términos. | ||
| + | *Las '''soluciones''' de la ecuación son los valores que deben tomar las letras para que se cumpla la igualdad. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| + | |||
| + | }} | ||
| + | |||
| ==Ecuaciones equivalentes== | ==Ecuaciones equivalentes== | ||
| {{Caja_Amarilla|texto=Dos ecuaciones son '''equivalentes''' si tienen las mismas soluciones.}} | {{Caja_Amarilla|texto=Dos ecuaciones son '''equivalentes''' si tienen las mismas soluciones.}} | ||
Revisión de 12:32 7 feb 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 176)
Ecuaciones e identidades
- Una ecuación es una igualdad entre expresiones algebraicas.
- Una identidad es una igualdad entre expresiones algebraicas que es cierta para cualquier valor que le demos a las letras que intervienen.
 es una ecuación pero no una identidad ya que sólo es cierta para
es una ecuación pero no una identidad ya que sólo es cierta para 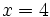
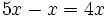 es una identidad ya que es cierta para cualquier valor que le demos a la letra
es una identidad ya que es cierta para cualquier valor que le demos a la letra 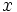 .
.
Elementos de una ecuación
Una ecuación es una igualdad entre dos expresiones algebraicas.
- A cada una de las dos expresiones algebraicas separadas por el signo igual se les llama miembros de la ecuación: el primer miembro es el que está a la izquierda de la igualdad y el segundo miembro el que está a la derecha.
- Cada uno de los sumandos que forman cada miembro de la ecuación se llaman términos de la ecuación.
- Las incógnitas son las letras que aparecen en los términos.
- Las soluciones de la ecuación son los valores que deben tomar las letras para que se cumpla la igualdad.
Ecuaciones equivalentes
Dos ecuaciones son equivalentes si tienen las mismas soluciones.
Resolver una ecuación
Resolver una ecuación es hallar su solución o soluciones, si es que existe alguna.
- Ecuaciones con una incógnita:
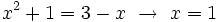 es una solución.
es una solución.
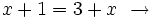 No tiene solución.
No tiene solución.
- Ecuación con dos incógnitas:
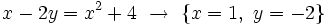 es una solución.
es una solución.
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones |

