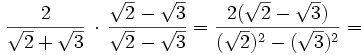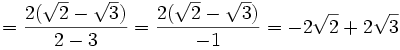Plantilla:Racionalizacion
De Wikipedia
| Revisión de 06:59 22 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:10 22 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| |sinopsis=Racionaliza: <math>\cfrac{4}{\sqrt{32}}</math>. | |sinopsis=Racionaliza: <math>\cfrac{4}{\sqrt{32}}</math>. | ||
| |url1=https://www.youtube.com/watch?v=SDU1h5aJgV0 | |url1=https://www.youtube.com/watch?v=SDU1h5aJgV0 | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 3 | ||
| + | |duracion=5'26" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{\sqrt{2}}{\sqrt{5}}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=R48mBL3EWrM | ||
| }} | }} | ||
| }} | }} | ||
| Línea 89: | Línea 95: | ||
| {{Videotutoriales|titulo=Racionalización (caso III)|enunciado= | {{Videotutoriales|titulo=Racionalización (caso III)|enunciado= | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Ejemplo | + | |titulo1=Ejemplo 1 |
| - | |duracion=6'31" | + | |duracion=7'26" |
| - | |sinopsis=Racionaliza: <math>\cfrac{5}{2\,\sqrt[3]{7}}</math>. | + | |sinopsis=Racionaliza: <math>\cfrac{3}{\sqrt{5}-\sqrt{2}}</math>. |
| - | |url1=https://www.youtube.com/watch?v=h7e7Tjq71gE | + | |url1=https://www.youtube.com/watch?v=FINVZJM6qp4 |
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 2 | ||
| + | |duracion=5'54" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{1}{\sqrt{7}+\sqrt{3}}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=dRC14JZQm3g | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 3 | ||
| + | |duracion=6'46" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{3}{3+\sqrt{5}}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=15qQkWBKk5U | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 4 | ||
| + | |duracion=6'20" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{2}{\sqrt{7}-1}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=ugUevR9931o | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 5 | ||
| + | |duracion=7'02" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{11}{2\sqrt{3}-1}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=C1YoAoBRYuo | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 6 | ||
| + | |duracion=6'43" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{4}{5\,\sqrt{2}+\sqrt{6}}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=aVZkdaGiGCA | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 7 | ||
| + | |duracion=7'43" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{12}{5\,\sqrt{6}-3\,\sqrt{10}}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=cs_m7DZFWC0 | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 8 | ||
| + | |duracion=7'05" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{\sqrt{5}}{\sqrt{3}-\sqrt{2}}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=Qt_k6oASEKU | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejemplo 9 | ||
| + | |duracion=9'20" | ||
| + | |sinopsis=Racionaliza: <math>\cfrac{\sqrt{5}-\sqrt{2}}{\sqrt{7}+\sqrt{5}}</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=WfkRNwyFBV8 | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 07:10 22 may 2017
Se llama racionalización al procedimiento por el cual a partir de una fracción con raíces en el denominador obtenemos otra fracción equivalente sin raíces en el denominador
Tabla de contenidos |
Caso 1: Denominador con raíces cuadradas
Para racionalizar un radical de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.
Ejemplo: Caso 1: Denominador con raíces cuadradas
Racionalizar 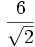
En este caso hay que multiplicar numerador y denominador por 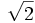
Caso 2: Denominador con otras raíces
En este caso, los exponentes del radicando del radical por el que se deben multiplicar el numerador y denominador de la fracción será la diferencia entre los exponentes actuales y el índice (o múltiplo del indice más cercano) del radical.
Ejemplo: Caso 2: Denominador con otras raíces
Racionalizar ![\frac{{2}}{\sqrt[5]{a^3b^4}}](/wikipedia/images/math/5/3/3/533185378740f77c6d3da802a18e1fdd.png)
En este ejemplo, hay que multiplicar numerador y denominador por ![\sqrt[5] {a^2b}](/wikipedia/images/math/3/d/5/3d57844c30135fee650c9bcfd98d40d1.png) , ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz:
, ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz:
Caso 3: Denominador con sumas y restas de raíces
Para este último caso, se multiplica y divide por la expresión conjugada del denominador (solo se le cambia el segundo signo de la expresión)
Ejemplo: Caso 3: Denominador con sumas y restas de raíces
Racionalizar 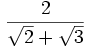
En este caso hay que multiplicar el numerador y el denominador por 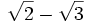 (este resultado es el que da el producto notable de los binomios conjugados):
(este resultado es el que da el producto notable de los binomios conjugados):
Racionaliza: 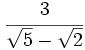 .
.
Racionaliza: 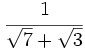 .
.
Racionaliza: 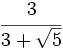 .
.
Racionaliza: 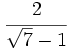 .
.
Racionaliza: 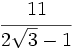 .
.
Racionaliza: 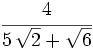 .
.
Racionaliza: 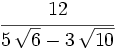 .
.
Racionaliza: 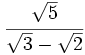 .
.
Racionaliza: 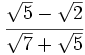 .
.
Actividades
4 ejemplos.
3 ejemplos.
1 ejemplo.
1 ejemplo.
1 ejercicio.
1 ejercicio.
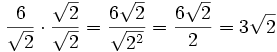
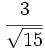 .
.
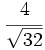 .
.
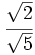 .
.
![\frac{{2}}{\sqrt[5]{a^3b^4}} \cdot \frac{\sqrt[5] {a^2b} }{\sqrt[5]{a^2b}} = \frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}} = \frac{{2\sqrt[5]{a^2b}}}{{ab}}](/wikipedia/images/math/0/a/6/0a6d73fa5ee1fe441c50539e138ae167.png)
![\cfrac{2}{\sqrt[4]{3}}](/wikipedia/images/math/3/6/3/363cdd6889755a849dc9a7ea0bac576d.png) .
.
![\cfrac{1}{\sqrt[5]{8}}](/wikipedia/images/math/b/a/0/ba08551ff4220087d9fbb68dee2ffd73.png) .
.
![\cfrac{5}{2\,\sqrt[3]{7}}](/wikipedia/images/math/8/3/b/83b21b3caaf20fd75d0e6b3f0a3cc8c3.png) .
.
![\cfrac{4}{\sqrt[5]{72}}](/wikipedia/images/math/6/b/b/6bb931ba83b1b6b45859a0561fd025ca.png) .
.