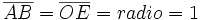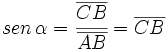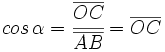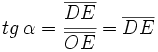Plantilla:Circunferencia goniométrica
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:04 22 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:22 24 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto=Llamaremos '''circunferencia goniométrica''' a la circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con centro en el origen de coordenadas, '''O'''. | {{Caja_Amarilla|texto=Llamaremos '''circunferencia goniométrica''' a la circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con centro en el origen de coordenadas, '''O'''. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=La circunferencia goniométrica | ||
| + | |duracion=7´01" | ||
| + | |url1=https://www.youtube.com/watch?v=svbJrQNEArk | ||
| + | |sinopsis=Definición y propiedades de la circunferencia goniométrica. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 10:22 24 may 2017
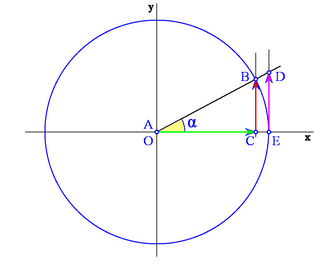
Llamaremos circunferencia goniométrica a la circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con centro en el origen de coordenadas, O.
Definición y propiedades de la circunferencia goniométrica.
Sobre la circunferencia goniométrica situaremos nuestro ángulo orientado, 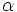 . Este genera un triángulo rectángulo ABC, tal y como se muestra en la Fig. 2. En él, el vértice A coincide con el origen O, el cateto contiguo al ángulo . Este genera un triángulo rectángulo ABC, tal y como se muestra en la Fig. 2. En él, el vértice A coincide con el origen O, el cateto contiguo al ángulo 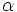 se situa en el eje X positivo y la hipotenusa coincide con el radio. se situa en el eje X positivo y la hipotenusa coincide con el radio.
Teniendo en cuenta que |
Empleando un circulo de radio unidad pueden "visualizarse" las razones trigonométricas de un ángulo orientado.
En este vídeo jugamos a dibujar un ángulo del que se conoce una de sus seis razones trigonométricas (seno, coseno, tangente, cotangente, secante y cosecante).