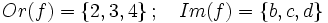Correspondencia
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:39 23 may 2017 Coordinador (Discusión | contribuciones) (→Tipos de correspondencias. Aplicaciones) ← Ir a diferencia anterior |
Revisión de 09:50 23 may 2017 Coordinador (Discusión | contribuciones) (→Tipos de correspondencias. Aplicaciones) Ir a siguiente diferencia → |
||
| Línea 61: | Línea 61: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Aplicaciones o funciones|enunciado= | + | {{Videotutoriales|titulo=Aplicación o función|enunciado= |
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| |titulo1=Función | |titulo1=Función | ||
Revisión de 09:50 23 may 2017
Correspondencia entre conjuntos
Una correspondencia ente dos conjuntos A y B es una ley o criterio que asocia elementos de A con elementos de B.
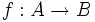
|
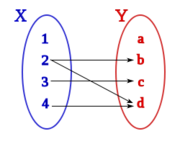
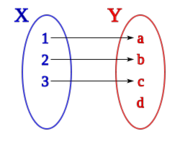
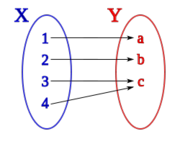
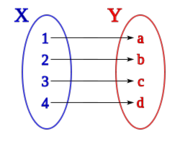
Sean los conjuntos X={1, 2, 3, 4} y Y={a, b, c, d}, una correspondencia, 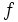 , entre X e Y podría ser aquella que asocia los elementos de X con los de Y siguiendo el siguiente diagrama de Venn:
, entre X e Y podría ser aquella que asocia los elementos de X con los de Y siguiendo el siguiente diagrama de Venn:
- Fíjate que en el conjunto inicial, X, puede haber elementos,
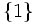 , que no tengan asignado ningún elemento del conjunto final, Y.
, que no tengan asignado ningún elemento del conjunto final, Y.
- Igualmente, puede haber elementos de Y,
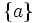 , a los que no se les ha asignado ningún elemento de X.
, a los que no se les ha asignado ningún elemento de X.
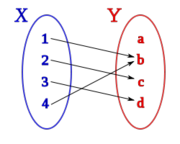
- En el conjunto inicial, X, puede haber elementos,
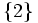 , a los que les correspondan más de un elemento de Y: f(2)=b; f(2)=d
, a los que les correspondan más de un elemento de Y: f(2)=b; f(2)=d
- Igualmente, puede haber elementos de Y,
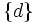 , a los que les corresponde más de un elmento de X: f(2)=d; f(4)=d
, a los que les corresponde más de un elmento de X: f(2)=d; f(4)=d
- Definición de correspondencia entre conjuntos.
- Conjunto inicial y conjunto final. Ejemplos.
El concepto de relación es sinónimo al de correspondencia.
Tipos de correspondencias. Aplicaciones
- Una correspondencia es unívoca si cada elemento inicial que tenga imagen solo tienen una imagen.
- Una correspondencia es biunívoca si cada elemento inicial que tenga imagen solo tienen una imagen, y cada elemento imagen solo tiene ese origen.
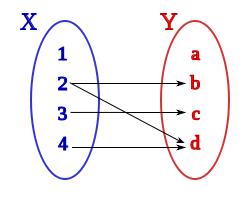
- Una aplicación o función es una correspondencia unívoca cuyo conjunto origen coincide con el conjunto inicial.
Concepto de función. Ejemplos.
Dominio y rango de una función. Ejemplos.
Cómo se evalua una función. Ejemplos.
Cómo se representa gráficamente una función. Ejemplos.
Tipos de aplicaciones
- Una aplicación es inyectiva si cada imagen se corresponde con un único origen.
- Una aplicación es sobreyectiva si el conjunto imagen coincide con el conjunto final.
- Una aplicación es biyectiva si es inyectiva y sobreyectiva simultaneamente.
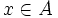 , al elemento de B que se corresponda con
, al elemento de B que se corresponda con  lo representaremos por
lo representaremos por  y se leerá "imagen de x según f ". (Notación introducida por
y se leerá "imagen de x según f ". (Notación introducida por 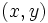 , con
, con 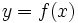 , a las parejas de elementos que estén en correspondencia mediante
, a las parejas de elementos que estén en correspondencia mediante 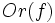 , de la correspondencia
, de la correspondencia 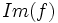 , de la correspondencia
, de la correspondencia