Plantilla:Paso de decimal a fraccion
De Wikipedia
| Revisión de 16:45 25 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:46 25 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| |titulo1=Paso de decimal exacto a fracción | |titulo1=Paso de decimal exacto a fracción | ||
| |duracion=6'29" | |duracion=6'29" | ||
| - | |sinopsis=Cómo se halla la fracción generatiz de un número decimal exacto. Ejemplos. | + | |sinopsis=Cómo obtener la fracción generatiz de un número decimal exacto. Ejemplos. |
| |url1=https://www.youtube.com/watch?v=0kXK41r--5U&t=295s | |url1=https://www.youtube.com/watch?v=0kXK41r--5U&t=295s | ||
| }} | }} | ||
| Línea 33: | Línea 33: | ||
| |duracion=5'56" | |duracion=5'56" | ||
| |sinopsis=Halla la fracción generatriz de los números: | |sinopsis=Halla la fracción generatriz de los números: | ||
| - | #<math>0.125\;</math> | + | :a) <math>0.125\;</math> |
| - | #<math>3.16\;</math> | + | :b) <math>3.16\;</math> |
| |url1=https://www.youtube.com/watch?v=sBPvZKBAN-8 | |url1=https://www.youtube.com/watch?v=sBPvZKBAN-8 | ||
| }} | }} | ||
Revisión de 16:46 25 may 2017
Paso de decimal exacto a fracción
La fracción generatriz de un decimal exacto tiene en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales.
Es consecuencia del siguiente procedimiento:
- Sea N el número decimal exacto.
- Multiplicamos N por 10 elevado al número de decimales.
- Despejamos N para obtener la fracción.
Cómo obtener la fracción generatiz de un número decimal exacto. Ejemplos.
Halla la fracción generatriz de los números:
- a)
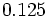
- b)
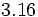
Paso de decimal periódico puro a fracción
La fracción generatriz de un número decimal periódico puro tiene como numerador la diferencia entre a y b, donde a es el número escrito sin la coma (sin repetir el periodo) y b es la parte entera del número; y como denominador, tantos "9" como cifras tiene el periodo.
Es consecuencia del siguiente procedimiento:
- Sea N el número decimal.
- Multiplicamos N por 10 elevado al número de cifras que tenga el periodo, lo que permite obtener otro número con la misma parte decimal.
- Restamos N y el número obtenido en el paso anterior.
- Despejando N llegamos a la fracción buscada.
Halla la fracción generatriz de los números periódicos puros:
- a) 1.6666...
- b) 2.646464...
Halla la fracción generatriz de número periódico puro 0.3636...
Halla la fracción generatriz de los siguientes números periódicos puros:
- a) 0.888...
- b) 0.212121...
- c) 0.537537537...
- d) 2.444...
- e) 10.484848...
Paso de decimal periódico mixto a fracción
La fracción generatriz de un número decimal periódico mixto tiene como numerador la diferencia entre a y b, donde a es el número escrito sin la coma (sin repetir el periodo) y b es el número escrito sin la coma quitándole la parte decimal periódica. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras tenga el anteperiodo.
Es consecuencia del siguiente procedimiento:
- Sea N el número decimal.
- Multiplicamos N por 10 elevado al número de cifras que tenga el periodo más el anteperiodo.
- Multiplicamos N por 10 elevado al número de cifras que tenga el anteperiodo, lo que permite obtener otro número con la misma parte decimal que el del paso 2.
- Restamos los números obtenidos en los pasos 2 y 3.
- Despejando N llegamos a la fracción buscada.
Halla la fracción generatriz de los siguientes números periódicos mixtos:
- a) 2.46666...
- b) 3.246262626...
Halla la fracción generatriz de número periódico mixto 0.4333...
Halla la fracción generatriz de los siguientes números periódicos mixtos:
- a) 0.5111...
- b) 0.935555...
- c) 3.8121212...
- d) 1.06434343...

