Ángulos

De Wikipedia

Revisión de 19:58 28 may 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior		Revisión de 17:12 29 may 2007 Coordinador (Discusión | contribuciones) (→Medida de ángulos) Ir a siguiente diferencia →
Línea 73:		Línea 73:
	Un minuto sexagesimal, a su vez, también se divide en otras unidades más pequeñas, llamadas '''segundos sexagesimales'''. Un minuto equivale a 60 segundos (1'=60").		Un minuto sexagesimal, a su vez, también se divide en otras unidades más pequeñas, llamadas '''segundos sexagesimales'''. Un minuto equivale a 60 segundos (1'=60").
		+
		+	==Operaciones con ángulos==
		+	===Suma===
		+	La medida del tiempo, igual que los ángulos, se realiza en el sistema sexagesimal. Analicemos el siguiente ejemplo:
		+
		+	{{Ejemplo
		+	|titulo=Ejemplo: ''Suma en el sistema sexagesimal''
		+	|enunciado=
		+	:Luis es un corredor de maratón que para entrenarse corrió dos días seguidos una maratón. Obtuvo los siguientes registros: el primer día corrió la maratón en 2 h 48 min 35 s; el segundo día, en 2 h 45 min 30 s. ¿Cuánto tiempo corrió Luis en ambos días?
		+	|sol=
		+	Si sumamos por separado las horas, los minutos y los segundos, resulta:
		+	<center><pre>
		+	2 h 48 min 35 s
		+	+ 2 h 45 min 30 s
		+	___________________
		+	4 h 93 min 65 s
		+	</pre></center>
		+
		+	Pero 65 segundos equivalen a 1 minuto (60 segundos) y 5 segundos, luego la suma se puede escribir así:
		+
		+	<center><pre>4 h 94 min 5 s</pre></center>
		+
		+	De la misma forma, 94 min equivalen a 1 hora y 34 minutos. Luego la suma es:
		+
		+	<center><pre>5 h 34 min 5 s</pre></center>
		+	}}
		+	{{p}}
		+
		+	Los mismos procedimientos hay que realizar para sumar ángulos.
		+
		+	{{AI2|titulo=Actividad Interactiva: ''Suma de ángulos''|cuerpo=
		+	{{ai_cuerpo
		+	|enunciado=1. Suma de ángulos en el sistema sexagesimal.
		+	|actividad=
		+	Realiza en tu cuaderno las siguientes sumas de ángulos:
		+
		+	:a) 56º 20' 40" + 37º 42' 15"
		+
		+	:b) 125º 15' 30" + 24º 50' 40"
		+
		+	:c) 33º 33' 33" + 17º 43' 34"
		+
		+	A continuación, construye en la siguiente escena los ángulos anteriores para comprobar los resultados obtenidos.
		+
		+	Los grados, minutos y segundos superiores corresponden a los del primer sumando y los inferiores a los del segundo sumando.
		+
		+	<center><iframe>
		+	url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/Medicion_de_angulos/angulo5_1.html
		+	width=500
		+	height=300
		+	name=myframe
		+	</iframe></center>
		+
		+	}}
		+	}}

---

Revisión de 17:12 29 may 2007

Tabla de contenidos 1 Ángulo 2 Tipos de ángulos 3 Medida de ángulos 3.1 Sistema sexagesimal 4 Operaciones con ángulos 4.1 Suma

Ángulo

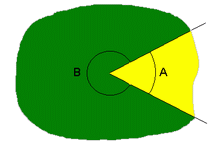
Un ángulo es la porción del plano comprendido entre dos semirrectas que tienen el mismo origen.

Dos semirrectas con un origen común determinan siempre dos porciones del plano y por tanto dos ángulos, A y B. Al ángulo A se le llama ángulo convexo, mientras que el ángulo B es cóncavo.

Tipos de ángulos

• Ángulo nulo

Es el ángulo definido por dos semirrectas que coinciden. No barre ninguna porción del plano.

• Ángulo recto

Es el ángulo convexo definido por dos semirrectas perpendiculares.

• Ángulo llano

Cuando las dos semirrectas que lo definen tienen la misma dirección, aunque sentidos opuestos. Barre un semiplano, esto es, la mitad del plano.

• Ángulo completo

Es el ángulo que abarca todo el plano.

• Ángulo agudo

Se llaman ángulos agudos a los que son menores que un ángulo recto.

• Ángulo obtuso

Se llaman ángulos obtusos a aquellos ángulos convexos (menores que un ángulo llano) que son mayores que un ángulo recto.

Actividad Interactiva: Ángulos 1. Animación que muestra los distintos tipos de ángulos. Actividad: Pulsa el botón de reproducción para ver la animación:

Medida de ángulos

Sistema sexagesimal

En este sistema la unidad es el grado sexagesimal y el ángulo completo tiene 360º.

El ángulo llano tiene 180º, porque es la mitad de un ángulo completo y el ángulo recto tiene 90º, porque es la mitad de un ángulo llano. Cuatro ángulos rectos forman un ángulo completo.

Actividad Interactiva: Sistema sexagesimal 1. Representación de ángulos. Actividad: Arrastra los puntos A y B de la escena para obtener los distintos ángulos: El ángulo se nombra siendo O el vértice, y A y B dos puntos en sus lados.

Un grado sexagesimal se divide en otras unidades más pequeñas llamadas minutos sexageximales. Un grado equivale a 60 minutos (1º=60').

Un minuto sexagesimal, a su vez, también se divide en otras unidades más pequeñas, llamadas segundos sexagesimales. Un minuto equivale a 60 segundos (1'=60").

Operaciones con ángulos

Suma

La medida del tiempo, igual que los ángulos, se realiza en el sistema sexagesimal. Analicemos el siguiente ejemplo:

Los mismos procedimientos hay que realizar para sumar ángulos.

Actividad Interactiva: Suma de ángulos 1. Suma de ángulos en el sistema sexagesimal. Actividad: Realiza en tu cuaderno las siguientes sumas de ángulos: a) 56º 20' 40" + 37º 42' 15" b) 125º 15' 30" + 24º 50' 40" c) 33º 33' 33" + 17º 43' 34" A continuación, construye en la siguiente escena los ángulos anteriores para comprobar los resultados obtenidos. Los grados, minutos y segundos superiores corresponden a los del primer sumando y los inferiores a los del segundo sumando.