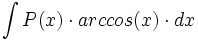Cálculo de primitivas por partes (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 06:07 26 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:11 26 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 15: | Línea 15: | ||
| {{p}} | {{p}} | ||
| {{ejemplo2 | {{ejemplo2 | ||
| - | |titulo=Ejemplos: ''Cálculo de primitivas por partes'' | + | |titulo=Ejercicios resueltos: ''Cálculo de primitivas por partes'' |
| - | |enunciado=:Primitivas del tipo <math>\int P(x) \cdot k^{ax} \cdot dx \quad k>0</math> donde <math>P(x)\;</math> es un polinomio. | + | |enunciado=Primitivas del tipo <math>\int P(x) \cdot k^{ax} \cdot dx \quad k>0</math> donde <math>P(x)\;</math> es un polinomio. |
| - | {{Video_enlace2 | + | {{Videotutoriales|titulo=Ejercicios|enunciado= |
| - | |titulo1=1. Ejemplos | + | {{Video_enlace_fonemato |
| - | |duracion=9'13" | + | |titulo1=Ejercicio 1 |
| + | |duracion=10'19" | ||
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cintegral/01/in01_06a_media/in01_06a.wmv | + | |url1=https://www.youtube.com/watch?v=GppwbEonobU&index=24&list=PLECA0C7A8B59E5534 |
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=7'08" | ||
| + | |sinopsis= | ||
| + | |url1=https://www.youtube.com/watch?v=kmpXk1i_Nx4&list=PLECA0C7A8B59E5534&index=25 | ||
| + | }} | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 06:11 26 jun 2017
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
- Deducción de la fórmula de integración "por partes".
- Casos típicos de aplicación.
Ejercicios resueltos: Cálculo de primitivas por partes
Primitivas del tipo 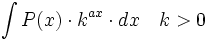 donde
donde 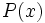 es un polinomio.
es un polinomio.
Ejemplos: Cálculo de primitivas por partes
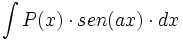 ó
ó 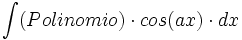 donde
donde 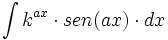 ó
ó 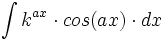
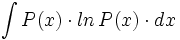
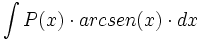 ó
ó