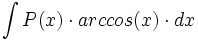Cálculo de primitivas por partes (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:38 26 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:40 26 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 24: | Línea 24: | ||
| #<math>\int x^2 \cdot e^x \cdot dx</math> | #<math>\int x^2 \cdot e^x \cdot dx</math> | ||
| #<math>\int x^3 \cdot e^x \cdot dx</math> | #<math>\int x^3 \cdot e^x \cdot dx</math> | ||
| - | #Determina las infinitas funciones cuya segunda derivada es <math>f''(x)=x \cdot e^x</math>, obteniendo la que pasa por el punto (0,2) y (2,0). | + | #Determina las infinitas funciones cuya segunda derivada es <math>f''(x)=x \cdot e^x</math>, obteniendo la que pasa por los puntos (0,2) y (2,0). |
| #<math>\int x^2 \cdot 3^x \cdot dx</math> | #<math>\int x^2 \cdot 3^x \cdot dx</math> | ||
| #<math>\int x^2 \cdot e^{3x} \cdot dx</math> | #<math>\int x^2 \cdot e^{3x} \cdot dx</math> | ||
Revisión de 07:40 26 jun 2017
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
- Deducción de la fórmula de integración "por partes".
- Casos típicos de aplicación.
Ejercicios resueltos: Cálculo de primitivas por partes
Primitivas del tipo 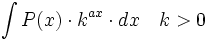 donde
donde 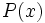 es un polinomio.
es un polinomio.
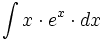
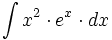
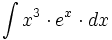
- Determina las infinitas funciones cuya segunda derivada es
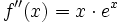 , obteniendo la que pasa por los puntos (0,2) y (2,0).
, obteniendo la que pasa por los puntos (0,2) y (2,0).
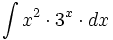
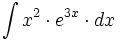
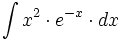
Ejemplos: Cálculo de primitivas por partes
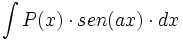 ó
ó 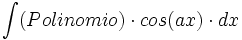 donde
donde 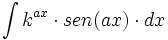 ó
ó 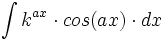
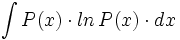
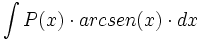 ó
ó