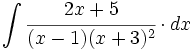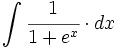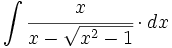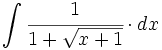Ejercicios: Cálculo de primitivas (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:32 27 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:45 27 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 59: | Línea 59: | ||
| |sinopsis=<math>\int \cfrac{1}{cos^4 \, x} \cdot dx</math> mediante cambio de variable <math>tg \, x = z</math>. | |sinopsis=<math>\int \cfrac{1}{cos^4 \, x} \cdot dx</math> mediante cambio de variable <math>tg \, x = z</math>. | ||
| |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/11-calculo-de-primitivas/009-ejercicio-9 | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/11-calculo-de-primitivas/009-ejercicio-9 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 10 | ||
| + | |duracion=3'41" | ||
| + | |sinopsis=Hallar <math>f: \mathbb{R} \rightarrow \mathbb{R}</math> tal que f(0)=0, f'(=)=5, f''(0)=1 y f'''(x)=x+1 | ||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/11-calculo-de-primitivas/010-ejercicio-7 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 11 | ||
| + | |duracion=3'41" | ||
| + | |sinopsis=<math>\int \cfrac{2x+5}{(x-1)(x+3)^2} \cdot dx</math> | ||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/11-calculo-de-primitivas/011-ejercicio-7 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 12 | ||
| + | |duracion=3'03" | ||
| + | |sinopsis=<math>\int \cfrac{1}{1+e^x} \cdot dx</math> | ||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/11-calculo-de-primitivas/012-ejercicio-7 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 13 | ||
| + | |duracion=2'06" | ||
| + | |sinopsis=<math>\int \cfrac{x}{x-\sqrt{x^2-1}} \cdot dx</math> | ||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/11-calculo-de-primitivas/013-ejercicio-7 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 14 | ||
| + | |duracion=1'55" | ||
| + | |sinopsis=<math>\int \cfrac{1}{1+\sqrt{x+1}} \cdot dx</math> | ||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/11-calculo-de-primitivas/014-ejercicio-7 | ||
| + | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 15 | ||
| + | |duracion=3'04" | ||
| + | |sinopsis=<math>\int (x^2 \cdot ln \, x -x \cdot ln \, x^2) \cdot dx</math> | ||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/11-calculo-de-primitivas/015-ejercicio-7 | ||
| }} | }} | ||
Revisión de 09:45 27 jun 2017
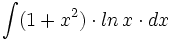
![\int \cfrac{1}{\sqrt[3]{x^2} \cdot (\sqrt[3]{x^2}+\sqrt[3]{x}+1)} \cdot dx](/wikipedia/images/math/b/a/5/ba5f7a6904dd982111c210de34296c2e.png)
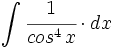 mediante cambio de variable
mediante cambio de variable 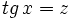 .
.
Hallar 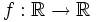 tal que f(0)=0, f'(=)=5, f(0)=1 y f'(x)=x+1
tal que f(0)=0, f'(=)=5, f(0)=1 y f'(x)=x+1