Polígonos (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:27 16 jul 2017 Coordinador (Discusión | contribuciones) (→Atendiendo al número de lados) ← Ir a diferencia anterior |
Revisión de 18:33 16 jul 2017 Coordinador (Discusión | contribuciones) (→Elementos de un polígono) Ir a siguiente diferencia → |
||
| Línea 34: | Línea 34: | ||
| {{Tabla50|celda1= | {{Tabla50|celda1= | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
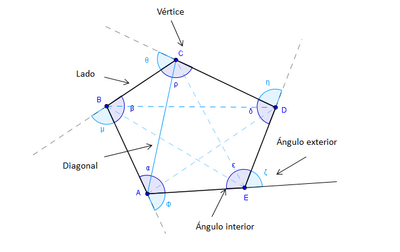
| - | *'''Lados''' del pológono: son los segmentos de la línea poligonal que lo conforma. | + | *'''Lados''' del polígono: son los segmentos de la línea poligonal que lo conforma. |
| *'''Vértices''' del polígono: son los extremos de los segmentos de la línea poligonal que lo conforma. | *'''Vértices''' del polígono: son los extremos de los segmentos de la línea poligonal que lo conforma. | ||
| *'''Diagonales''' del polígono: son los segmentos que unen dos vértices no consecutivos dl polígono. | *'''Diagonales''' del polígono: son los segmentos que unen dos vértices no consecutivos dl polígono. | ||
| - | *'''Ángulos''' del polígono: son los ángulos entre cada dos segmentos consecutivos del polígono. Pueden ser '''interiores''' o '''exteriores''' al polígono. | + | *'''Ángulos''' del polígono: son los ángulos entre cada dos segmentos consecutivos del polígono. Pueden ser: |
| + | **'''Interiores''': si quedan dentro del polígono. | ||
| + | **'''Exteriores''': si están formados por un lado de un polígono y la prolongación del lado adyacente. | ||
| }} | }} | ||
| |celda2=[[Imagen:elem_ploigono.png|center|400px]]}} | |celda2=[[Imagen:elem_ploigono.png|center|400px]]}} | ||
Revisión de 18:33 16 jul 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Juega al tangram de cinco piezas.
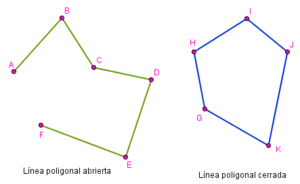
Línea poligonal
|
Polígono
|
Elementos de un polígono
|
Clasificicación de los polígonos
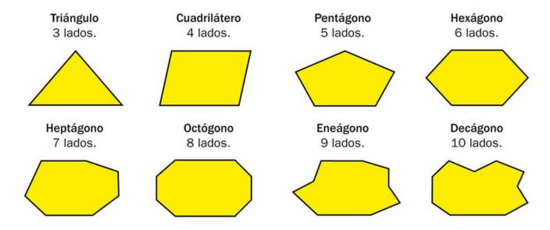
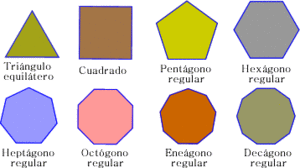
Atendiendo al número de lados
|
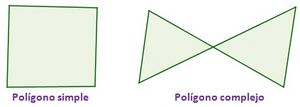
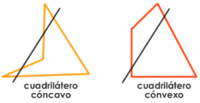
Atendiendo a su contorno
|
Atendiendo a su regularidad
|