Plantilla:Figuras semejantes
De Wikipedia
| Revisión de 17:26 25 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:30 25 jul 2017 Coordinador (Discusión | contribuciones) (→Figuras semejantes) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Figuras semejantes''|cuerpo= | + | {{AI_enlace|titulo1=Figuras semejantes |
| - | + | url=http://maralboran.org/web_ma/geometria/geoweb/semej1_1.html | |
| - | {{ai_cuerpo | + | |descripcion= |
| - | |enunciado=1. Comprueba las propiedades de dos figuras semejantes. | + | |
| - | |actividad= | + | |
| Observa los dos polígonos de la figura. Se dice que son semejantes porque cumplen las dos condiciones antes mencionadas: | Observa los dos polígonos de la figura. Se dice que son semejantes porque cumplen las dos condiciones antes mencionadas: | ||
| Línea 36: | Línea 34: | ||
| </iframe></center> | </iframe></center> | ||
| }} | }} | ||
| - | }} | + | |
| ===Escala=== | ===Escala=== | ||
| Ya hemos visto antes que escala y razón de semejanza significan lo mismo. El término escala suele utilizarse en planos o mapas. Así, por ejemplo, decimos que un plano está a escala 1:100 si 1 cm en el plano son 100 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es <math>r=\cfrac{1}{100}</math>. | Ya hemos visto antes que escala y razón de semejanza significan lo mismo. El término escala suele utilizarse en planos o mapas. Así, por ejemplo, decimos que un plano está a escala 1:100 si 1 cm en el plano son 100 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es <math>r=\cfrac{1}{100}</math>. | ||
Revisión de 17:30 25 jul 2017
Figuras semejantes
De manera intuitiva, dos figuras son semejantes si tienen la misma forma, pero el tamaño es diferente.
Matematicamente, dos figuras semejantes cumplen:
- Los ángulos correspondientes son iguales (misma forma).
- Los segmentos correspondientes son proporcionales.
Se llama razón de semejanza o escala,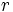 
, al cociente entre dos longitudes correspondientes.
[{{{url1}}} Figuras semejantes
url=http://maralboran.org/web_ma/geometria/geoweb/semej1_1.html] Descripción: Observa los dos polígonos de la figura. Se dice que son semejantes porque cumplen las dos condiciones antes mencionadas:
- Los ángulos correspondientes son todos iguales.
- Los segmentos correspondientes son proporcionales.
En efecto,
1. Los ángulos son iguales ya que los lados correspondientes son paralelos.
2. Para comprobar que los lados son proporcionales usa los segmentos MN y XY que puedes mover libremente. Mide con ellos dos segmentos correspondientes AB y A'B' por ejemplo y calcula la razón de semejanza.
Mueve ahora el punto rojo para comprobar el valor de r.
Escala
Ya hemos visto antes que escala y razón de semejanza significan lo mismo. El término escala suele utilizarse en planos o mapas. Así, por ejemplo, decimos que un plano está a escala 1:100 si 1 cm en el plano son 100 cm en la realidad. Es lo mismo que decir que la razón de semejanza entre la figura dibujada y la real es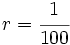 
.
Problema 1 (3'50") Sinopsis:En una fotografía, la imagen de un persona mide 12 cm, ¿qué escala se ha utilizado si la persona mide en realidad 1.80 m?.
Problema 2 (2'41") Sinopsis:Los planos de un juguete están a escala 1:10. ¿Cuál es la longitud del juguete si en el plano mide 8 cm?.
