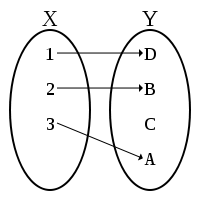
Función inyectiva
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:16 25 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 16: | Línea 16: | ||
| ---- | ---- | ||
| - | b) Al restringir el dominio a números positivos, dado cualquier valor de la imagen , solo existe un valor del dominio (su raíz cuadrada positiva) que se corresponde con él. | + | b) Al restringir el dominio a números positivos, dado cualquier valor de la imagen , solo existe un valor del dominio, su raíz cuadrada positiva, que se corresponde con él. |
| }} | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
Una función 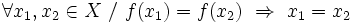 Ejemplo: Función inyectiva
Solución: a) En efecto, la función no es inyectiva puesto que b) Al restringir el dominio a números positivos, dado cualquier valor de la imagen , solo existe un valor del dominio, su raíz cuadrada positiva, que se corresponde con él. |
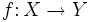 es inyectiva o uno a uno si cada valor en la imagen de
es inyectiva o uno a uno si cada valor en la imagen de 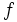 se corresponde con un único valor de
se corresponde con un único valor de 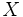 . Simbólicamente:
. Simbólicamente:
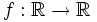 , dada por
, dada por 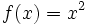 no es inyectiva
no es inyectiva
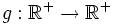 entonces sí se obtiene una función inyectiva.
entonces sí se obtiene una función inyectiva.
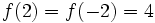 . Es decir, hay dos valores del dominio, 2 y -2, cuya imagen coincide (4).
. Es decir, hay dos valores del dominio, 2 y -2, cuya imagen coincide (4).