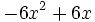Plantilla:Factorización de polinomios de grado 2
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:29 2 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 32: | Línea 32: | ||
| |duracion=8'02" | |duracion=8'02" | ||
| |sinopsis=Descomposición factorial de polinomios de grado 2 resolviendo la ecuación de segundo grado. | |sinopsis=Descomposición factorial de polinomios de grado 2 resolviendo la ecuación de segundo grado. | ||
| - | |url1=https://www.youtube.com/watch?v=-KoB6FycTO4&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=2&t=1m53s | + | |url1=http://www.youtube.com/watch?v=-KoB6FycTO4&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=2&t=1m53s |
| }} | }} | ||
| ---- | ---- | ||
| Línea 43: | Línea 43: | ||
| :5b) <math>2x^2+2x-4\;</math> | :5b) <math>2x^2+2x-4\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=kGXX7ubcfi8&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=14 | + | |url1=http://www.youtube.com/watch?v=kGXX7ubcfi8&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=14 |
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| Línea 53: | Línea 53: | ||
| :5d) <math>x^2+3x+2\;</math> | :5d) <math>x^2+3x+2\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=w2KftAazafw&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=15 | + | |url1=http://www.youtube.com/watch?v=w2KftAazafw&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=15 |
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| Línea 63: | Línea 63: | ||
| :5f) <math>-x^2+3x+10\;</math> | :5f) <math>-x^2+3x+10\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=tV8yq2NA2_I&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=16 | + | |url1=http://www.youtube.com/watch?v=tV8yq2NA2_I&list=PLw7Z_p6_h3oxSJsFvVwzC47s98v2d3ja9&index=16 |
| }} | }} | ||
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
Revisión actual
Factorización de polinomios de segundo grado
Un polinomio de segundo grado, 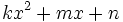 , con raíces rales,
, con raíces rales,  y
y 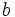 , se puede factorizar de la forma
, se puede factorizar de la forma
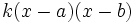
Ejemplos: Factorización de polinomios de segundo grado y reducibles
Factoriza los siguientes polinomios
- a)
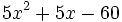
- b)
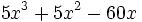
Solución:
- El polinomio
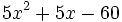 tiene dos raíces:
tiene dos raíces: 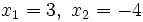 , que se obtienen de resolver la ecuación de segundo grado
, que se obtienen de resolver la ecuación de segundo grado 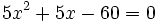 . Entonces:
. Entonces:
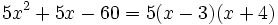
- El polinomio incompleto de grado 3,
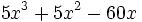 , se puede descomponer de la siguiente manera:
, se puede descomponer de la siguiente manera:
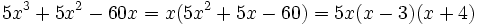
- (Observa que primero hemos sacado factor común
 y luiego hemos factorizado el polinomio de grado 2, como hicimos en el ejemplo anterior).
y luiego hemos factorizado el polinomio de grado 2, como hicimos en el ejemplo anterior).
Descomposición factorial de polinomios de grado 2 resolviendo la ecuación de segundo grado.
Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5a)
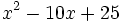
- 5b)
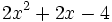
Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5c)
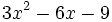
- 5d)
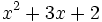
Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- 5e)
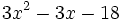
- 5f)
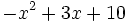
Factoriza los siguientes polinomios de segundo grado resolviendo la ecuación de 2º grado:
- a)
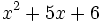
- b)
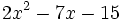
- c)
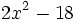
- d)