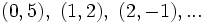Sistemas de ecuaciones de primer grado
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:46 5 jul 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:48 5 jul 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 43: | Línea 43: | ||
| Las soluciones vienen dadas por las parejas <math>(x,y)\;\!</math> así obtenidas: | Las soluciones vienen dadas por las parejas <math>(x,y)\;\!</math> así obtenidas: | ||
| <center><math>(0,5),\ (1,2),\ (2,-1),...</math></center> | <center><math>(0,5),\ (1,2),\ (2,-1),...</math></center> | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | {{Caja_Amarilla|texto= | ||
| - | Toda '''ecuación de primer grado con una incógnita''' se puede reducir a la forma: | ||
| - | <center><math>ax+b=0\;\!</math>{{p}}</center> | ||
| - | Si <math>a \ne 0</math>, la ecuación tiene como única solución: <math>x= -\cfrac{b}{a}</math>. | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Solución de una ecuación de primer grado con una incógnita''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Ejemplos de soluciones de ecuaciones de primer grado con una incógnita. | ||
| - | |actividad= | ||
| - | Pulsa los botones para ver más ecuaciones. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_sol_ej.html | ||
| - | width=700 | ||
| - | height=290 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | }} | ||
| - | }} | ||
| - | ==Ecuaciones equivalentes== | ||
| - | {{Caja_Amarilla|texto=Dos ecuaciones son '''equivalentes''' si tienen la misma solución.}}{{p}} | ||
| - | ===Transformaciones que mantienen la equivalencia de las ecuaciones=== | ||
| - | {{Caja_Amarilla|texto= | ||
| - | *'''Sumar o restar la misma expresión en los dos miembros de la igualdad'''. Así, lo que está sumando en un miembro, pasa restando al otro miembro. Y viceversa. | ||
| - | *'''Multiplicar o dividir los dos miembros de la igualdad por un mismo número distinto de cero'''. Así, lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa. | ||
| - | }} | ||
| - | |||
| - | ==Resolución de ecuaciones de primer grado== | ||
| - | Para resolver una ecuación, hay que transformarla en otras ecuaciones equivalentes, cada vez más sencillas, hasta conseguir despejar la incógnita. Usaremos las transformaciones descritas en el apartado anterior. | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Resolución de ecuaciones de primer grado''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Ecuaciones de primer grado sencillas (resueltas). | ||
| - | |actividad= | ||
| - | Pulsa el botón EJEMPLO para ver más ecuaciones. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_sfp_ej.html | ||
| - | width=700 | ||
| - | height=230 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2:''' Ecuaciones de primer grado con paréntesis (resueltas). | ||
| - | |actividad= | ||
| - | Pulsa el botón EJEMPLO para ver más ecuaciones. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_p_ej.html | ||
| - | width=700 | ||
| - | height=260 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 3:''' Ecuaciones de primer grado con denominadores (resueltas). | ||
| - | |actividad= | ||
| - | Pulsa el botón EJEMPLO para ver más ecuaciones. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_f_ej.html | ||
| - | width=700 | ||
| - | height=260 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | ==Resolución de problemas mediante ecuaciones de primer grado== | ||
| - | Para resolver un problema mediante una ecuación, hay que seguir los siguientes pasos: | ||
| - | |||
| - | #Determinar la incógnita. | ||
| - | #Expresar el enunciado del problema en lenguaje algebraico, es decir, escribir una ecuación en la que intervenga la incógnita. | ||
| - | #Resolver la ecuación, es decir, halla el valor de la incógnita. | ||
| - | #Dar la solución del problema, a partir del valor obtenido de la incógnita. | ||
| - | <br> | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Resolución de problemas mediante ecuaciones de primer grado''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Problemas resueltos. | ||
| - | |actividad= | ||
| - | Pulsa el botón EJEMPLO para ver más problemas. | ||
| - | Pulsa el botón DATOS para ver otro problema similar, pero con datos diferentes. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/ecuaciones_primer_grado/ecua_pr_ej_1.html | ||
| - | width=700 | ||
| - | height=350 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 17:48 5 jul 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas es aquella que se puede expresar de la forma:
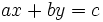
donde 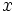 e
e 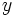 son variables y
son variables y 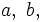 y
y 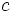 constantes.
constantes.
Ejemplo: 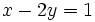
Soluciones de una ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas tiene infinitas soluciones. Para cada valor que le asignemos a la variable 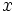 , podemos encontrar un valor de la variable
, podemos encontrar un valor de la variable 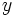 despejándola en la ecuación.
despejándola en la ecuación.
Ejemplo: Ecuación de primer grado con dos incógnitas
- Halla algunas soluciones para la ecuación:
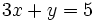
Solución:
Despejamos la variable y:
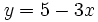
Construimos una tabla de valores, dandole valores a 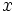 y calculando
y calculando 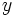 en la expresión anterior:
en la expresión anterior:
| x | 0 | 1 | 2 | ... |
| y | 5 | 2 | -1 | ... |
Las soluciones vienen dadas por las parejas 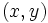 así obtenidas:
así obtenidas: