Números racionales: Orden
De Wikipedia
| Revisión de 11:24 7 ago 2007 Coordinador (Discusión | contribuciones) (→Ejercicios) ← Ir a diferencia anterior |
Revisión de 18:05 3 oct 2007 Coordinador (Discusión | contribuciones) (→Orden en el conjunto de los racionales) Ir a siguiente diferencia → |
||
| Línea 31: | Línea 31: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/fracciones/valor2_1.html | + | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/fracciones/valor2_1b.html |
| width=500 | width=500 | ||
| height=280 | height=280 | ||
| Línea 40: | Línea 40: | ||
| }} | }} | ||
| }} | }} | ||
| + | |||
| ==Ejercicios== | ==Ejercicios== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 18:05 3 oct 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Números decimales | WIRIS Geogebra Calculadora Fracciones |
Orden en el conjunto de los racionales
De dos fracciones con el mismo denominador, es mayor la de mayor numerador. Por eso, para ordenar fracciones, debemos primero obtener fracciones equivalentes a las dadas, pero con el mismo denominador. A ésto se le llama reducir a común denominador. Veamos un ejemplo:
Ejemplo: Ordenar fracciones
- Ordena las fracciones:
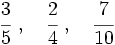
Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:
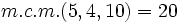 .
.Obtenemos fracciones equivalentes a las dadas con denominador 20. Para ello dividimos 20 entre cada denominador y lo multiplicamos por el numerador. Las fracciones obtenidas son:
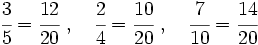
Estas fracciones las podemos ordenar fácilmente porque tienen el mismo denominador:
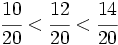
Así obtenemos:
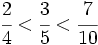
|
Actividad Interactiva: Ordenar fracciones
Actividad 1: Ordena de menor a mayor estas fracciones.
Actividad: Coloca estas fracciones ordenadas de menor a mayor. Pulsa "inicio" para que aparezcan otras fracciones. |
Ejercicios
|
Ejercicios: Ordenar fracciones 1. Ordena de menor a mayor las fracciones: Solución: 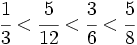 |