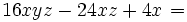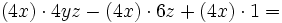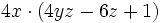Polinomios
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:27 1 oct 2007 Coordinador (Discusión | contribuciones) (→Suma y resta de polinomios) ← Ir a diferencia anterior |
Revisión de 18:28 1 oct 2007 Coordinador (Discusión | contribuciones) (→Sacar factor común) Ir a siguiente diferencia → |
||
| Línea 47: | Línea 47: | ||
| ===Sacar factor común=== | ===Sacar factor común=== | ||
| + | La propiedad distributiva sirve para simplificar expresiones '''sacando factor común'''. Veamos un ejemplo | ||
| + | {{p}} | ||
| + | {{Ejemplo | ||
| + | |titulo=Ejemplo: ''Sacar factor común'' | ||
| + | |enunciado= | ||
| + | :Saca factor común en la expresión <math>16xyz-24xz+4x\;\!</math> | ||
| + | |sol= | ||
| + | El factor común, que se repite en los tres sumandos, es <math>4x\,\!</math>. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común <math>4x\,\!</math>, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:{{p}} | ||
| + | <center><math>16xyz-24xz+4x\;\!=</math>{{p}} | ||
| + | <math>(4x) \cdot 4yz - (4x) \cdot 6z + (4x) \cdot 1=\;\!</math>{{p}} | ||
| + | <math>4x \cdot (4yz-6z+1)</math></center> | ||
| + | }} | ||
Revisión de 18:28 1 oct 2007
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Polinomios
- Un polinomio es una expresión algebraica que se obtiene al sumar dos o mas monomios. A cada monomio se le llama un término del polinomio. Si tiene dos términos se llama binomio; si tiene tres trinomio, etc.
- Se llama forma reducida de un polinomio a aquella en la que se ha simplificado, sumando los términos semejantes.
- Se llama grado de un polinomio al mayor de los grados de los monomios que lo componen cuando el polinomio se ha puesto en forma reducida.
- Un número se dice que es una raíz de un polinomio si el valor numérico del polinomio para dicho número es cero.
Ejemplos:
- a) El polinomio
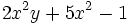 está en forma reducida y es un trinomio de grado 3.
está en forma reducida y es un trinomio de grado 3.
- b) El polinomio
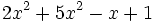 no está en forma reducida. Su forma reducida es
no está en forma reducida. Su forma reducida es 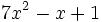 .
.
- c) El número
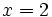 es una raíz del polinomio
es una raíz del polinomio 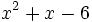
Operaciones con polinomios
Suma y resta de polinomios
Para sumar o restar polinomios, sumaremos o restaremos los monomios semejantes de ambos.
Ejemplos:
- a)
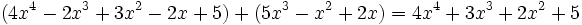
- b)
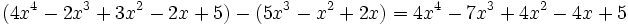
Producto de un monomio por un polinomio
Para multiplicar un monomio por un polinomio, se multiplica el monomio por cada término del polinomio y se suman los resultados.
Ejemplo:
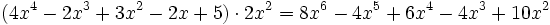
Producto de polinomios
Para multiplicar dos polinomios, se multiplica cada monomio de uno de sus factores por todos y cada uno de los monomios del otro factory, después, se suman los monomios semejantes obtenidos.
Ejemplo:
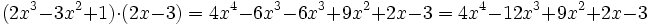
Sacar factor común
La propiedad distributiva sirve para simplificar expresiones sacando factor común. Veamos un ejemplo
Ejemplo: Sacar factor común
- Saca factor común en la expresión
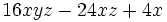
Solución:
El factor común, que se repite en los tres sumandos, es
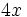 . Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 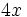 , dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso: