Transformaciones elementales de funciones (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:55 23 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:58 23 ene 2009 Coordinador (Discusión | contribuciones) (→Traslación vertical) Ir a siguiente diferencia → |
||
| Línea 13: | Línea 13: | ||
| |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> cualquiera y de su transformada <math>f(x) \pm k</math>. | |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> cualquiera y de su transformada <math>f(x) \pm k</math>. | ||
| |actividad= | |actividad= | ||
| - | En esta escena tienes la gráfica de la función <math>f(x) = x^2\;</math> y la de de f(x)+1=x^2+1\;. Prueba a introducir otras funciones: f(x)+2, f(x)-3 y compáralas con f(x). | + | En esta escena tienes la gráfica de la función <math>f(x) = x^2\;</math> y la de de <math>f(x)+1=x^2+1\;</math>. Prueba a introducir otras funciones: f(x)+2, f(x)-3 y compáralas con f(x). |
| {{p}} | {{p}} | ||
Revisión de 07:58 23 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Geogebra Calculadoras |
Traslación vertical
Sea  una función y
una función y 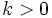 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 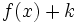 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola 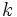 unidades hacia arriba y la de
unidades hacia arriba y la de 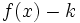 desplazándola k unidades hacia abajo.
desplazándola k unidades hacia abajo.
|
Actividad Interactiva: Traslación vertical de una función
Actividad 1. Representación gráfica de una función
 cualquiera y de su transformada cualquiera y de su transformada 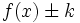 . .Actividad: En esta escena tienes la gráfica de la función 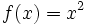 y la de de y la de de 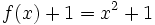 . Prueba a introducir otras funciones: f(x)+2, f(x)-3 y compáralas con f(x). . Prueba a introducir otras funciones: f(x)+2, f(x)-3 y compáralas con f(x).
|

