Plantilla:Dominio e imagen de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:24 1 feb 2009 Coordinador (Discusión | contribuciones) (→Razones para restringir el dominio de una función) ← Ir a diferencia anterior |
Revisión de 20:53 1 feb 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace2 | + | |
| - | |titulo1=Dominio de definición de una función | + | |
| - | |duracion=8'51" | + | |
| - | |sinopsis= | + | |
| - | *Dominio de definición de una función. | + | |
| - | *Interpretación gráfica del dominio. | + | |
| - | *Necesidad de saber el dominio de una función. | + | |
| - | *Ejemplos. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0134.htm | + | |
| - | }} | + | |
| - | {{p}} | + | |
| {{AI2|titulo=Actividad Interactiva: ''Dominio e imagen''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Dominio e imagen''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| Línea 60: | Línea 50: | ||
| *Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos) | *Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos) | ||
| *Por voluntad de quien propone la función. | *Por voluntad de quien propone la función. | ||
| - | {{p}} | ||
| - | {{Video_enlace2 | ||
| - | |titulo1=Reglas "Sagradas" del Cálculo | ||
| - | |duracion=3'43" | ||
| - | |sinopsis= | ||
| - | *Hay ciertas reglas en matemáticas que no se pueden violar. Aquí las vamos a recordar. | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0132.htm | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo | {{Ejemplo | ||
Revisión de 20:53 1 feb 2009
Dominio e imagen de una función
- Al conjunto de los valores que puede tomar la variable independiente
 , se le llama dominio de definición de la función. Lo representaremos por
, se le llama dominio de definición de la función. Lo representaremos por 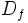 ó
ó 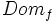
- La imagen, rango o recorrido de una función es el conjunto de valores que puede tomar la variable dependiente
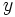 . Lo representaremos por
. Lo representaremos por 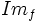 o
o 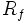 .
.
|
Actividad Interactiva: Dominio e imagen
1. Determina el dominio y la imagen de las siguientes funciones.
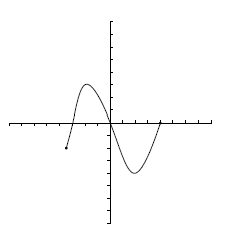
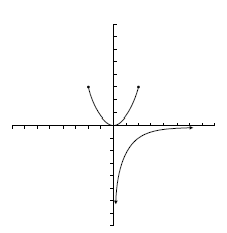
Actividad: a) Observa la escena y mueve el punto P para ver los valores que recorren las variables: Suponiendo que la gráfica se comporta de forma análoga a lo largo de todo el eje X,¿Cuál es su dominio y su imagen? b) Observa esta otra escena y procedede como antes: ¿Cuál es su dominio y su imagen? c) Haz lo mismo con esta tercera escena: |
Razones para restringir el dominio de una función
- Imposibilidad de realizar alguna operación con ciertos valores de
 (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos,...)
(Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos,...)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos)
- Por voluntad de quien propone la función.
Ejemplo: Dominio de definición de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
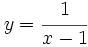
- b)
- c)
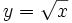
- c)
- d)
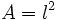 (Área de un cuadrado de lado
(Área de un cuadrado de lado 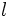 )
)
- d)
Solución:
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de 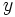 válido.
válido.
- b) Su dominio es
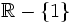 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
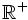 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
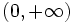 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
|
Ejercicios: Dominio e imagen |
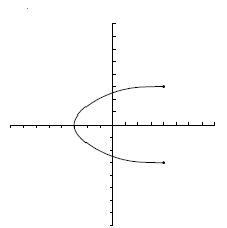
![D=[-3.5, 4]\;\!](/wikipedia/images/math/6/f/4/6f4030ef099e99944025cbb34e75c6ae.png) .
. ![Im=[-4, 3]\;\!](/wikipedia/images/math/4/9/c/49cf9064f7a20c06eb8cb9c71af85beb.png) .
.

