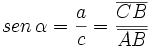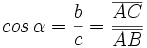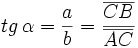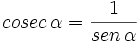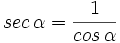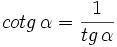Razones trigonométricas de un ángulo agudo (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:20 20 feb 2009 Coordinador (Discusión | contribuciones) (→Razones trigonométricas) ← Ir a diferencia anterior |
Revisión de 12:27 20 feb 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| == Razones trigonométricas == | == Razones trigonométricas == | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | {{Tabla3|celda3= | + | {{Tabla75|celda2= |
| <center>[[Image:Trigono b00.png|280px]]</center> | <center>[[Image:Trigono b00.png|280px]]</center> | ||
| |celda1= | |celda1= | ||
| Línea 14: | Línea 14: | ||
| * El '''seno''' (abreviado como ''sen'', o ''sin'' por llamarse "sinus" en latín) es la razón entre el cateto opuesto y la hipotenusa:{{p}} | * El '''seno''' (abreviado como ''sen'', o ''sin'' por llamarse "sinus" en latín) es la razón entre el cateto opuesto y la hipotenusa:{{p}} | ||
| - | {{Caja|contenido=<center><math> sen \, \alpha= \frac{a}{c} = \frac{\overline{CB}}{\overline{AB}} </math></center>}} | + | ::<math> sen \, \alpha= \frac{a}{c} = \frac{\overline{CB}}{\overline{AB}} </math> |
| * El '''coseno''' (abreviado como ''cos'') es la razón entre el cateto adyacente (o contiguo) y la hipotenusa:{{p}} | * El '''coseno''' (abreviado como ''cos'') es la razón entre el cateto adyacente (o contiguo) y la hipotenusa:{{p}} | ||
| - | {{Caja|contenido=<center><math> cos \, \alpha= \frac{b}{c} = \frac{\overline{AC}}{\overline{AB}} </math></center>}} | + | ::<math> cos \, \alpha= \frac{b}{c} = \frac{\overline{AC}}{\overline{AB}} </math> |
| * La '''tangente''' (abreviado como ''tan'' o ''tg'') es la razón entre el cateto opuesto y el cateto adyacente:{{p}} | * La '''tangente''' (abreviado como ''tan'' o ''tg'') es la razón entre el cateto opuesto y el cateto adyacente:{{p}} | ||
| - | {{Caja|contenido=<center><math> tg \, \alpha= \frac{a}{b} = \frac{\overline{CB}}{\overline{AC}} </math></center>}} | + | ::<math> tg \, \alpha= \frac{a}{b} = \frac{\overline{CB}}{\overline{AC}} </math> |
| - | |celda2={{p}} | + | }} |
| - | :Y las razones trigonométricas inversas: | + | }} |
| + | {{p}} | ||
| + | ===Razones trigonométricas inversas=== | ||
| + | {{Caja_Amarilla|texto=Las '''razones trigonométricas inversas''' se definen de la siguiente manera: | ||
| + | * La '''cosecante''' (abreviado como ''cosec''), inversa del seno:{{p}} | ||
| + | ::<math> cosec \, \alpha= \frac{1}{sen \, \alpha} </math> | ||
| - | :* El '''cosecante''' (abreviado como ''cosec''), inversa del seno:{{p}} | + | * La '''secante''' (abreviado como ''sec''), inversa del coseno:{{p}} |
| - | {{Caja|contenido=<center><math> cosec \, \alpha= \frac{1}{sen \, \alpha} </math></center>}} | + | ::<math> sec \, \alpha= \frac{1}{cos \, \alpha} </math> |
| - | :* El '''secante''' (abreviado como ''sec''), inversa del coseno:{{p}} | + | * La '''cotangente''' (abreviado como ''cotan'' o ''cotg''), inversa de la tangente:{{p}} |
| - | {{Caja|contenido=<center><math> sec \, \alpha= \frac{1}{cos \, \alpha} </math></center>}} | + | ::<math> cotg \, \alpha= \frac{1}{tg \, \alpha} </math> |
| - | :* La '''cotangente''' (abreviado como ''cotan'' o ''cotg''), inversa de la tangente:{{p}} | ||
| - | {{Caja|contenido=<center><math> cotg \, \alpha= \frac{1}{tg \, \alpha} </math></center>}} | ||
| - | |||
| - | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 12:27 20 feb 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
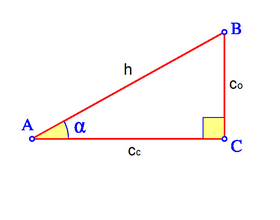
Razones trigonométricas
Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo 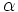 , de la siguiente manera: , de la siguiente manera:
|
Razones trigonométricas inversas
Las razones trigonométricas inversas se definen de la siguiente manera:
- La cosecante (abreviado como cosec), inversa del seno:
- La secante (abreviado como sec), inversa del coseno:
- La cotangente (abreviado como cotan o cotg), inversa de la tangente: