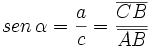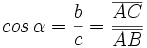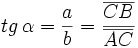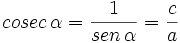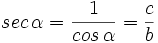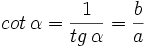Razones trigonométricas de un ángulo agudo (1ºBach)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 15:10 20 feb 2009
Coordinador (Discusión | contribuciones)
(→Ejercicios)
← Ir a diferencia anterior		 Revisión de 15:21 20 feb 2009
Coordinador (Discusión | contribuciones)
(→Razones trigonométricas)
Ir a siguiente diferencia →
Línea 9: Línea 9:
{{Caja_Amarilla|texto= {{Caja_Amarilla|texto=
{{Tabla75|celda2= {{Tabla75|celda2=
-<center>[[Image:Trigono b00.png|280px]]</center>+<center>[[Image:Trigono b00.png|300px]]</center>
|celda1= |celda1=
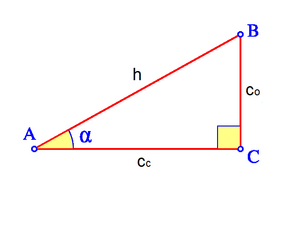
Dado un triángulo rectángulo ABC, se definen las '''razones trigonométricas''' del ángulo <math> \alpha \, </math>, de la siguiente manera: Dado un triángulo rectángulo ABC, se definen las '''razones trigonométricas''' del ángulo <math> \alpha \, </math>, de la siguiente manera:
Línea 34: Línea 34:
}} }}
{{p}} {{p}}
 +
==Razones trigonométricas recíprocas== ==Razones trigonométricas recíprocas==
{{Caja_Amarilla|texto=Las '''razones trigonométricas inversas''' se definen de la siguiente manera: {{Caja_Amarilla|texto=Las '''razones trigonométricas inversas''' se definen de la siguiente manera:

Revisión de 15:21 20 feb 2009

Menú:
Enlaces internos Para repasar o ampliar Enlaces externos
Indice
Descartes
Manual Casio
 WIRIS
Geogebra
Calculadoras

Tabla de contenidos

Razones trigonométricas

Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo 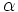\alpha \,, de la siguiente manera:
  • El seno (abreviado como sen, o sin por llamarse "sinus" en latín) es la razón entre el cateto opuesto y la hipotenusa:

sen \, \alpha= \frac{a}{c} = \frac{\overline{CB}}{\overline{AB}}
  • El coseno (abreviado como cos) es la razón entre el cateto adyacente (o contiguo) y la hipotenusa:

cos \, \alpha= \frac{b}{c} = \frac{\overline{AC}}{\overline{AB}}
  • La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto y el cateto adyacente:

tg \, \alpha= \frac{a}{b} = \frac{\overline{CB}}{\overline{AC}}

ejercicio
Ejemplos

Razones trigonométricas recíprocas

Las razones trigonométricas inversas se definen de la siguiente manera:

  • La cosecante (abreviado como csc o cosec), razón recíproca del seno:

cosec \, \alpha= \frac{1}{sen \, \alpha} = \frac{c}{a}
  • La secante (abreviado como sec), razón recíproca del coseno:

sec \, \alpha= \frac{1}{cos \, \alpha} = \frac{c}{b}
  • La cotangente (abreviado como cot), razón recíproca de la tangente:

cot \, \alpha= \frac{1}{tg \, \alpha} = \frac{b}{a}

ejercicio

Actividad interactiva: Razones trigonométricas

Actividad 1: Practica con las razones trigonométricas y ponte a prueba con una autoevaluación
Actividad:

  • Si pulsas el botón "EJERCICIO" cambiarán los datos del triángulo.
  • Si pulsas el botón "ángulo" cambiará el ángulo al que se le calculan las razones trigonométricas.
  • Si pulsas el botón "OTRAS RAZONES" alternararás entre las razones trigonométricas y sus recíprocas.
  • Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
Click aquí si no se ve bien la escena

Relaciones fundamentales de la trigonometría

ejercicio

Relaciones fundamentales de la trigonometría

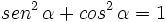
1. sen^2 \, \alpha + cos^2 \, \alpha = 1

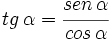
2. tg \, \alpha =\cfrac{sen \, \alpha }{cos \, \alpha}
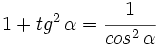
3. 1+tg^2 \, \alpha =\cfrac{1}{cos^2 \, \alpha}
Demostración:

1. sen^2 \, \alpha + cos^2 \, \alpha = \left ( \cfrac{a}{c} \right )^2 + \left ( \cfrac{b}{c} \right )^2 =\cfrac {a^2+b^2}{c^2}= \cfrac {c^2}{c^2}=1

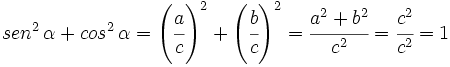
ya que, por el teorema de Pitágoras, 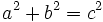a^2+b^2=c^2\;.


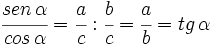
2. \cfrac{sen \, \alpha }{cos \, \alpha}=\cfrac{a}{c}:\cfrac{b}{c}=\cfrac{a}{b}=tg \, \alpha


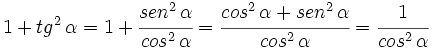
3. 1+tg^2 \, \alpha =1+\cfrac{sen^2 \, \alpha }{cos^2 \, \alpha}=\cfrac{cos^2 \, \alpha + sen^2 \, \alpha}{cos^2 \, \alpha}=\cfrac{1}{cos^2 \, \alpha}

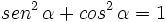
donde en el último paso hemos utilizado la primera relación fundamental: sen^2 \, \alpha + cos^2 \, \alpha = 1

Ejercicios

ejercicio

Ejercicios: Relaciones fundamentales de la trigonometría

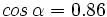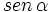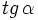1. Sabiendo que cos \, \alpha = 0.86, calcula sen \, \alpha y tg \, \alpha.
Solución:
sen \, \alpha = 0.51

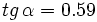
tg \, \alpha=0.59
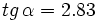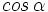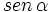2. Sabiendo que tg \, \alpha= 2.83, calcula cos \, \alpha y sen \, \alpha
Solución: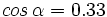
cos \, \alpha = 0.33

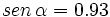sen \, \alpha=0.93
Obtenido de "http://www.maralboran.org/wikipedia/index.php/Razones_trigonom%C3%A9tricas_de_un_%C3%A1ngulo_agudo_%281%C2%BABach%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda