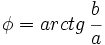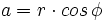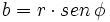Números complejos: Forma polar (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:29 9 mar 2009 Coordinador (Discusión | contribuciones) (→Paso de forma binómica a polar) ← Ir a diferencia anterior |
Revisión de 16:39 9 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 34: | Línea 34: | ||
| }} | }} | ||
| - | ==Paso de forma polar a binómica== | + | ==Paso de forma polar a binómica. Forma trigonométrica de un complejo== |
| + | {{Caja_Amarilla|texto= | ||
| + | Dado un número complejo <math>r_\phi \,</math>, su forma binómica <math>a+bi\,</math> se obtiene de la siguiente manera: | ||
| + | |||
| + | *<math>a=r \cdot cos \, \phi</math> | ||
| + | *<math>b=r \cdot sen \, \phi</math> | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | Según ésto: | ||
| + | |||
| + | <math>z=a+bi= r \cdot cos \, \phi + r \cdot sen \, \phi \cdot i=r \, (cos \, \phi + i \, sen \, \phi)</math> | ||
| + | {{p}} | ||
| + | {{Caja_Amarilla|texto= | ||
| + | |||
| + | A la expresión <math>z=r \, (cos \, \phi + i \, sen \, \phi)</math> se le llama '''forma trigonométrica''' del número complejo. | ||
| + | |||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | ||
Revisión de 16:39 9 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
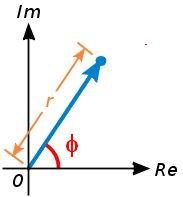
Módulo y argumento de un número complejo. Forma polar de un complejo
Paso de forma binómica a polar
Dado un número complejo 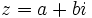 su forma polar su forma polar 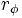 se obtiene de la siguiente manera: se obtiene de la siguiente manera:
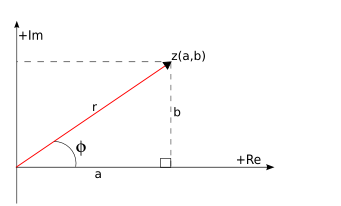
| 
|
Paso de forma polar a binómica. Forma trigonométrica de un complejo
Dado un número complejo 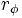 , su forma binómica
, su forma binómica 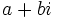 se obtiene de la siguiente manera:
se obtiene de la siguiente manera:
Según ésto:

A la expresión 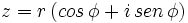 se le llama forma trigonométrica del número complejo.
se le llama forma trigonométrica del número complejo.
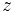 es la longitud del vector que lo representa, es decir, la distancia entre el afijo
es la longitud del vector que lo representa, es decir, la distancia entre el afijo 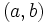 y el origen
y el origen 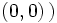 . Se designa por
. Se designa por 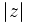 .
.
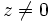 ), es el ángulo que forma el vector con el eje X . Se designa por
), es el ángulo que forma el vector con el eje X . Se designa por 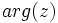 . (Si
. (Si 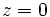 , su argumento es 0).
, su argumento es 0).
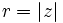 y
y 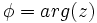 .
.
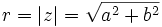 (por el
(por el