La circunferencia (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 22:01 23 mar 2009 Coordinador (Discusión | contribuciones) (→Ecuación de la circunferencia) ← Ir a diferencia anterior |
Revisión de 22:12 23 mar 2009 Coordinador (Discusión | contribuciones) (→Ecuación de la circunferencia) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| {{p}} | {{p}} | ||
| {{Caja_Amarilla|texto= La ecuación de la circunferencia de centro <math>O(a,b)\,</math> y radio <math>r\,</math>, es: | {{Caja_Amarilla|texto= La ecuación de la circunferencia de centro <math>O(a,b)\,</math> y radio <math>r\,</math>, es: | ||
| + | {{p}} | ||
| <center><math>\sqrt{(x-a)^2+(y-b)^2}=r</math></center> | <center><math>\sqrt{(x-a)^2+(y-b)^2}=r</math></center> | ||
| Línea 21: | Línea 22: | ||
| {{p}} | {{p}} | ||
| {{Teorema|titulo=Proposición|enunciado=La ecuación de una circunferencia de centro <math>O(a,b)\,</math> y radio <math>r\,</math>, es: | {{Teorema|titulo=Proposición|enunciado=La ecuación de una circunferencia de centro <math>O(a,b)\,</math> y radio <math>r\,</math>, es: | ||
| + | |||
| <center><math>x^2+y^2+Ax+By+C=0 \,</math></center> | <center><math>x^2+y^2+Ax+By+C=0 \,</math></center> | ||
| - | donde <math>A=-2a \, , \; B=-2b \, , \; C=a^2+b^2-r^2</math> | + | |
| + | donde: <math>A=-2a \, , \; B=-2b \, , \; C=a^2+b^2-r^2</math>. | ||
| |demo=Partiendo de la ecuación de la circunferencia: | |demo=Partiendo de la ecuación de la circunferencia: | ||
| - | <center><math>\sqrt{(x-a)^2+(y-b)^2}=r</math></center> | + | <center><math>\sqrt{(x-a)^2+(y-b)^2}=r\,</math></center> |
| Elevando al cuadrado ambos términos: | Elevando al cuadrado ambos términos: | ||
| - | <center><math>(x-a)^2+(y-b)^2=r^2</math></center> | + | <center><math>(x-a)^2+(y-b)^2=r^2\,</math></center> |
| y desarrollando el radicando: | y desarrollando el radicando: | ||
| - | <center><math>x^2-2ax+a^2+y^2-2by+b^2=r^2</math></center> | + | <center><math>x^2-2ax+a^2+y^2-2by+b^2=r^2\,</math></center> |
| Agrupando términos: | Agrupando términos: | ||
| - | <center><math>x^2+y^2-2ax-2bx+a^2+b^2-r^2=0</math></center> | + | <center><math>x^2+y^2-2ax-2bx+a^2+b^2-r^2=0\,</math></center> |
| + | |||
| y llamando <math>A=-2a \, , \; B=-2b \, , \; C=a^2+b^2-r^2</math>, se tiene la ecuación. | y llamando <math>A=-2a \, , \; B=-2b \, , \; C=a^2+b^2-r^2</math>, se tiene la ecuación. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema|titulo=Corolario|enunciado=Dada la circunferencia de ecuación <math>x^2+y^2+Ax+By+C=0 \,</math>, su centro y su radio son: | + | {{Teorema|titulo=Corolario|enunciado=Dada la circunferencia de ecuación {{sube|porcentaje=+10%|contenido=<math>x^2+y^2+Ax+By+C=0 \,</math>}}, su centro y su radio vienen dados por: |
| - | <center><math>O(-\cfrac{A}{2},-\cfrac{B}{2}) \quad , \quad r=\sqrt{\big( \cfrac{A}{2} \big)^2+\cfrac{B}{2} \big)^2}-C</math>. | + | <center><math>O(-\cfrac{A}{2},-\cfrac{B}{2}) \quad , \quad r=\sqrt{\big( \cfrac{A}{2} \big)^2+\cfrac{B}{2} \big)^2-C}</math>. |
| |demo=Es inmediato a partir de la proposición anterior, despejando <math>a\,</math>, <math>b\,</math> y <math>r\,</math>. | |demo=Es inmediato a partir de la proposición anterior, despejando <math>a\,</math>, <math>b\,</math> y <math>r\,</math>. | ||
| }} | }} | ||
Revisión de 22:12 23 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Circunferencia
La circunferencia de centro 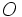 y radio
y radio 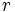 , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 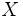 , cuya distancia al centro es
, cuya distancia al centro es 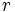 .
.
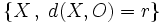
Ecuación de la circunferencia
De la anterior definición, utilizando la fórmula de la distancia entre dos puntos, tenemos:
La ecuación de la circunferencia de centro 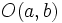 y radio
y radio 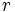 , es:
, es:

Proposición
La ecuación de una circunferencia de centro 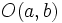 y radio
y radio 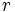 , es:
, es:
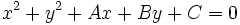
donde: 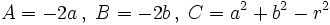 .
.
Demostración:
Partiendo de la ecuación de la circunferencia:

Elevando al cuadrado ambos términos:
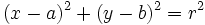
y desarrollando el radicando:
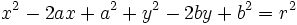
Agrupando términos:
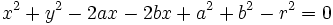
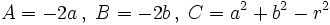 , se tiene la ecuación.
, se tiene la ecuación.Corolario
Dada la circunferencia de ecuación 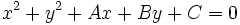 , su centro y su radio vienen dados por:
, su centro y su radio vienen dados por:
 .
.
Demostración:
Es inmediato a partir de la proposición anterior, despejando
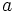 ,
, 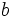 y
y 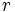 .
.
