Plantilla:Discriminante de la ecuación de segundo grado
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 13:05 30 ago 2016 Coordinador (Discusión | contribuciones) (→Discriminante de una ecuación de segundo grado) ← Ir a diferencia anterior |
Revisión de 13:26 30 ago 2016 Coordinador (Discusión | contribuciones) (→Discriminante de una ecuación de segundo grado) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Proposición | + | {{Teorema|titulo=Proposición |
| |enunciado=:Sea <math>\triangle</math> el discriminante de una ecuación de segundo grado: | |enunciado=:Sea <math>\triangle</math> el discriminante de una ecuación de segundo grado: | ||
| Línea 12: | Línea 12: | ||
| :*Si <math>\triangle >0</math>, la ecuación tiene dos soluciones. | :*Si <math>\triangle >0</math>, la ecuación tiene dos soluciones. | ||
| :*Si <math>\triangle =0</math>, la ecuación tiene una solución (doble). | :*Si <math>\triangle =0</math>, la ecuación tiene una solución (doble). | ||
| + | |||
| + | |demo= La demostración es inmediata teniendo en cuenta la fórmula para la resolución de la ecuación de segundo grado: | ||
| + | <br> | ||
| + | <center><math>x=\cfrac{-b \pm \sqrt {b^2-4ac}}{2a}</math></center> | ||
| + | |||
| + | ya que, lo que hay en el radicando, es precisamente el discriminante. Por tanto, | ||
| + | |||
| + | * Si su signo es positivo, la raíz existe y da lugar a dos soluciones distintas. | ||
| + | * Si su signo es negativo, la raíz no existe y no hay ninguna solución. | ||
| + | * Si es cero, la raíz vale cero, y hay dos soluciones iguales (solución doble). | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 13:26 30 ago 2016
Discriminante de una ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado, 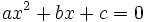 , al número:
, al número:
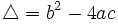
Proposición
- Sea
 el discriminante de una ecuación de segundo grado:
el discriminante de una ecuación de segundo grado:
- Si
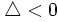 , la ecuación no tiene solución.
, la ecuación no tiene solución.
- Si
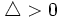 , la ecuación tiene dos soluciones.
, la ecuación tiene dos soluciones.
- Si
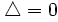 , la ecuación tiene una solución (doble).
, la ecuación tiene una solución (doble).
- Si
Demostración:
La demostración es inmediata teniendo en cuenta la fórmula para la resolución de la ecuación de segundo grado:
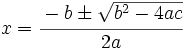
ya que, lo que hay en el radicando, es precisamente el discriminante. Por tanto,
- Si su signo es positivo, la raíz existe y da lugar a dos soluciones distintas.
- Si su signo es negativo, la raíz no existe y no hay ninguna solución.
- Si es cero, la raíz vale cero, y hay dos soluciones iguales (solución doble).
|
Actividad Interactiva: Discriminante de una ecuación de segundo grado
Calcula el discriminante de las siguientes ecuaciones de segundo grado.
Actividad:
|

