El significado de las fracciones (1º ESO)
De Wikipedia
| Revisión de 11:32 25 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:36 25 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 43: | Línea 43: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/ciclo1/fracciones/anaya/01.htm | + | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/01.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/ciclo1/fracciones/anaya/01.htm | + | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/01.htm |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 56: | Línea 56: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/ciclo1/fracciones/anaya/02.htm | + | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/02.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/ciclo1/fracciones/anaya/02.htm | + | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/02.htm |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 125: | Línea 125: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/ciclo1/fracciones/anaya/03.htm | + | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/03.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/ciclo1/fracciones/anaya/03.htm | + | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/03.htm |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 171: | Línea 171: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/ciclo1/fracciones/anaya/05.htm | + | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/05.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/ciclo1/fracciones/anaya/05.htm | + | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/05.htm |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:36 25 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 122)
Las fracciones
Cuando necesitamos expresar cantidades con partes de la unidad, además de los números decimales, disponemos de las fracciones.
- Una fracción es un número que expresa una cantidad determinada de porciones que se toman de un todo dividido en partes iguales. Se representa
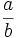 , o bien,
, o bien, 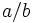 :
:
- A
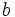 se le llama denominador y representa las partes en que se divide la unidad.
se le llama denominador y representa las partes en que se divide la unidad.
- A
- A
 se le llama numerador y representa las porciones que tomamos.
se le llama numerador y representa las porciones que tomamos.
- A
- El valor de la fracción es el número que resulta de dividir el numerador entre el denominador.
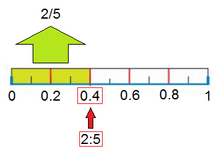
En la Fig. 1 tienes algunos ejemlos de fracciones representadas mendiante los llamados diagramas de tarta.
El valor de cada fracción se obtiene dividiendo el numerador entre el denominador:
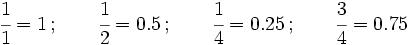
Fíjate que la unidad se puede representar mediante una fracción que tenga el mismo numerador que denominador.
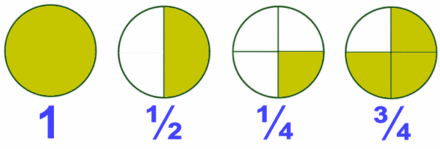
En la Fig. 2 está representada la fracción 2/5. Fíjate como al hacer la división 2:5=0.4, se obtienen 4 décimas, que ocupan la misma porción que la fracción 2/5. Es decir, una fracción equivale a una división indicada.
Fracciones propias e impropias
Proposición Toda fracción impropia se puede expresar como un número entero más una fracción propia, es decir, como número mixto. |
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
La fracción como operador
Procedimiento
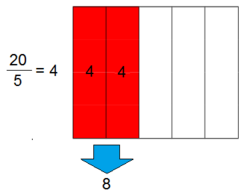
Para calcular la fracción de una cantidad, se divide la cantidad entre el denominador y se multiplica por el numerador.
Ejercicio resuelto: La fracción como operador
Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito?
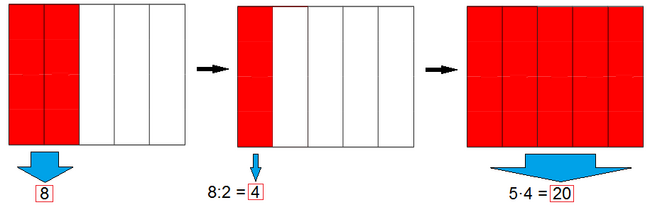
Ejemplo: La fracción como operador (problema inverso)
Un depósito de agua tiene 8 l, que son las 2/5 partes de su capacidad. ¿Cuál es la capacidad total del depósito?
Ejercicios propuestos
|
Ejercicios propuestos: El significado de las fracciones |
Problemas
|
Ejercicios propuestos: Problemas con fracciones |
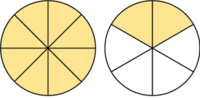
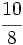 es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3):
es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3):
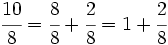
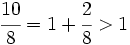
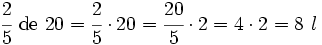
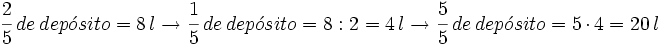
 = capacidad del depósito.
= capacidad del depósito.