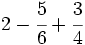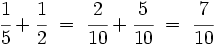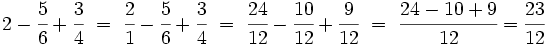Fracciones: Suma y resta (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:11 25 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión de 17:16 25 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 29: | Línea 29: | ||
| {{p}} | {{p}} | ||
| ==Suma y resta de fracciones con distinto denominador== | ==Suma y resta de fracciones con distinto denominador== | ||
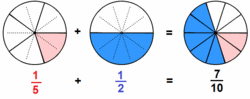
| + | {{Tabla75|celda2=[[Imagen:suma_frac_dist_den.gif|thumb|250px|Fig.1: Suma de fracciones con distinto denominador]] | ||
| + | |celda1= | ||
| {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Para sumar o restar fracciones con distinto denominador, primero se reducen las fracciones a común denominador y luego se procede como en el caso en el que las fracciones tienen el mismo denominador.}} | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Para sumar o restar fracciones con distinto denominador, primero se reducen las fracciones a común denominador y luego se procede como en el caso en el que las fracciones tienen el mismo denominador.}} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplos: ''Suma y resta de fracciones con distinto denominador''|enunciado= | {{Ejemplo|titulo=Ejemplos: ''Suma y resta de fracciones con distinto denominador''|enunciado= | ||
| - | :a) <math>\cfrac{2}{6}+\cfrac{4}{8}</math>{{b4}}{{b4}} b) <math>2-\cfrac{5}{6}+\cfrac{3}{4}</math> | + | :a) <math>\cfrac{1}{5}+\cfrac{1}{2}</math>{{b4}}{{b4}} b) <math>2-\cfrac{5}{6}+\cfrac{3}{4}</math> |
| |sol= | |sol= | ||
| - | a) m.c.m.(6, 8) = 24 | + | a) m.c.m.(5, 2) = 10 |
| - | <center><math>\cfrac{2}{6}+\cfrac{4}{8} \ = \ \cfrac{8}{24} + \cfrac{12}{24} \ = \ \cfrac{20}{24}</math></center> | + | <center><math>\cfrac{1}{5}+\cfrac{1}{2} \ = \ \cfrac{2}{10} + \cfrac{5}{10} \ = \ \cfrac{7}{10}</math></center> |
| {{b4}} | {{b4}} | ||
| Línea 44: | Línea 46: | ||
| <center><math>2-\cfrac{5}{6}+\cfrac{3}{4} \ = \ \cfrac{2}{1}-\cfrac{5}{6}+\cfrac{3}{4} \ = \ \cfrac{24}{12}-\cfrac{10}{12}+\cfrac{9}{12} \ = \ \cfrac{24-10+9}{12} =\cfrac{23}{12}</math></center> | <center><math>2-\cfrac{5}{6}+\cfrac{3}{4} \ = \ \cfrac{2}{1}-\cfrac{5}{6}+\cfrac{3}{4} \ = \ \cfrac{24}{12}-\cfrac{10}{12}+\cfrac{9}{12} \ = \ \cfrac{24-10+9}{12} =\cfrac{23}{12}</math></center> | ||
| }} | }} | ||
| - | + | }} | |
| {{p}} | {{p}} | ||
| {{AI_enlace | {{AI_enlace | ||
Revisión de 17:16 25 sep 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 138)
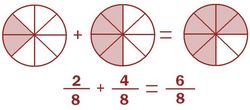
Suma y resta de fracciones con el mismo denominador
Procedimiento Para sumar o restar fracciones con el mismo denominador, sumamos o restamos los numeradores y dejamos el mismo denominador |
Suma y resta de fracciones con distinto denominador
Procedimiento Para sumar o restar fracciones con distinto denominador, primero se reducen las fracciones a común denominador y luego se procede como en el caso en el que las fracciones tienen el mismo denominador. |
Ejercicios propuestos
|
Ejercicios propuestos: Suma y resta de fracciones |
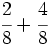 b)
b) 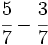
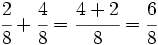
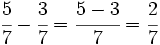
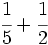 b)
b)