Distancias en el plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:40 14 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:46 14 oct 2016 Coordinador (Discusión | contribuciones) (→Distancia de un punto a una recta) Ir a siguiente diferencia → |
||
| Línea 54: | Línea 54: | ||
| ya que <math>Ax_0+By_0=-C\,</math>, por ser <math>R(x_0,y_0)\,</math> un punto de la recta. | ya que <math>Ax_0+By_0=-C\,</math>, por ser <math>R(x_0,y_0)\,</math> un punto de la recta. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo | ||
| + | |titulo=Ejercicio resuelto: ''Distancias en el plano'' | ||
| + | |enunciado=Halla el área del triángulo de vértices A(0,0), B(6,5) y C(2,5). | ||
| + | |sol= | ||
| + | Tomando como base del triángulo el lado BC, tendremos que calcular d(B,C) y d(A, BC) para hallar las medidas de la base y de la altura. | ||
| + | |||
| + | '''Solución:''' Área=10 u<sup>2</sup>. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 152: | Línea 161: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Distancia entre dos rectas== | ==Distancia entre dos rectas== | ||
| {{Video_enlace | {{Video_enlace | ||
Revisión de 17:46 14 oct 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 203)
Distancia ente dos puntos
La distancia entre dos puntos 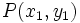 y
y 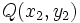 es igual al módulo del vector
es igual al módulo del vector 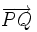 :
:
|
|
|
Actividad Interactiva: Distancia entre dos puntos
Actividad 1: En esta escena vamos a hallar la distancia entre los puntos
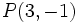 y y 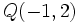 . .Actividad: 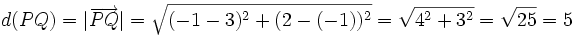
Ejercicio: Calcula la distancia entre los puntos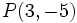 y y 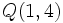 y comprueba el resultado en la escena anterior. y comprueba el resultado en la escena anterior. |
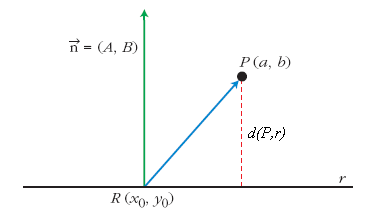
Distancia de un punto a una recta
Proposición
- La distancia del punto
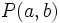 a la recta
a la recta 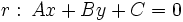 es:
es:
|
|
Ejercicio resuelto: Distancias en el plano
Halla el área del triángulo de vértices A(0,0), B(6,5) y C(2,5).
Solución:
Tomando como base del triángulo el lado BC, tendremos que calcular d(B,C) y d(A, BC) para hallar las medidas de la base y de la altura.
Solución: Área=10 u2.Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
|
Actividad Interactiva: Distancia de un punto a una recta
Actividad 1: En esta escena vamos a hallar la distancia del punto
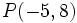 a la recta a la recta 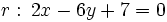 . .Actividad: 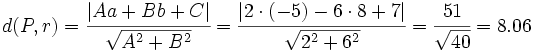
Ejercicio: Calcula la distancia del punto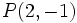 a la recta a la recta 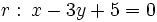 y comprueba el resultado en la escena anterior. y comprueba el resultado en la escena anterior. |
Distancia entre dos rectas
Videotutorial
Videotutorial
Bisectrices del ángulo entre dos rectas
Videotutorial
Videotutorial
Videotutorial
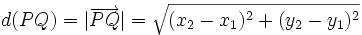
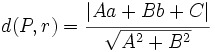
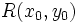 un punto de la recta.
un punto de la recta.
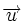
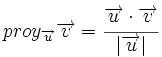
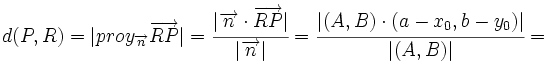
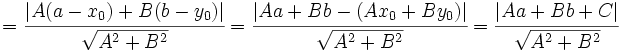
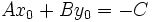 , por ser
, por ser 
