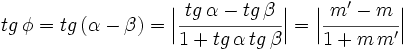Ángulo entre dos rectas del plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:36 14 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:42 15 oct 2016 Coordinador (Discusión | contribuciones) (→Ángulo entre dos rectas a partir de sus pendientes) Ir a siguiente diferencia → |
||
| Línea 74: | Línea 74: | ||
| }} | }} | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás calcular el ángulo entre dos rectas. | ||
| + | |enlace=[https://ggbm.at/aN4z3FsT Ángulo entre dos rectas] | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| ==Videotutoriales== | ==Videotutoriales== | ||
| {{p}} | {{p}} | ||
Revisión de 09:42 15 oct 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 202)
Ángulo entre dos rectas
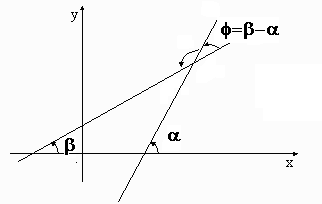
El ángulo entre dos rectas del plano es el menor de los dos ángulos que forman éstas entre sí.
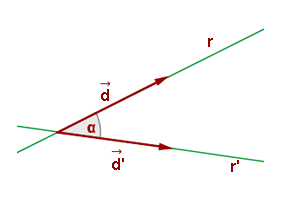
Ángulo entre dos rectas a partir de sus vectores de dirección
Ejemplo: Ángulo entre dos rectas
Halla el ángulo que forman las siguientes rectas:
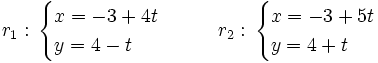
Solución:
Sus vectores de dirección son: 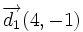 y
y 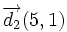 , de manera que:
, de manera que:
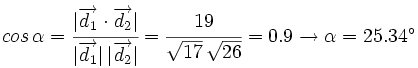
Ángulo entre dos rectas dadas en forma implícita
Proposición
Sean 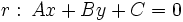 y
y 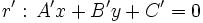 dos rectas, y sea
dos rectas, y sea 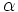 el ángulo que forman. Se verifica que
el ángulo que forman. Se verifica que
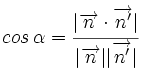
- donde
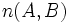 y
y 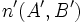 son los vectores normales de las rectas.
son los vectores normales de las rectas.
Demostración:
Cómo el vector normal a una recta es perpendicular al vector de dirección de la misma, hallar el ángulo entre las dos rectas equivale a hallar el ángulo entre los vectores normales o entre los vectores de dirección. Por tanto aplicaremos la misma fórmula que para hallar el ángulo a partir de los vectores de dirección, sustituyendo éstos por los vectores normales.
Ángulo entre dos rectas a partir de sus pendientes
Proposición
Dadas dos rectas con pendientes 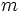 y
y 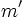 . Se verifica que
. Se verifica que
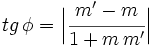
En esta escena podrás calcular el ángulo entre dos rectas.
Videotutoriales
- Ángulo entre dos rectas.
- Paralelismo y perpendicularidad.
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Ejercicios propuestos
|
Ejercicios propuestos: Ecuaciones trigonométricas |
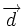
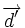
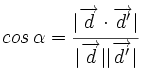
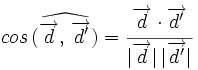
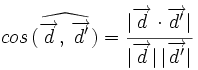
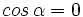 , de donde
, de donde 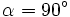 .
.
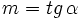 y
y 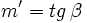 , usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos:
, usando la fórmula de la tangente de la diferencia de dos ángulos, tenemos: