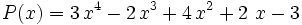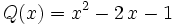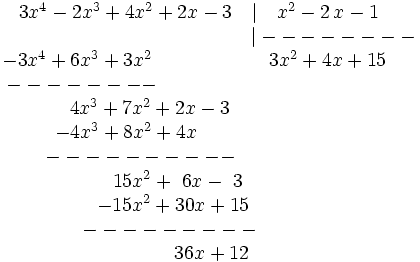Plantilla:División de polinomios

De Wikipedia

(Diferencia entre revisiones)
Revisión de 15:36 26 oct 2016
Coordinador (Discusión | contribuciones)

← Ir a diferencia anterior		 Revisión de 16:37 26 oct 2016
Coordinador (Discusión | contribuciones)

Ir a siguiente diferencia →
Línea 45: Línea 45:
\quad \ 36x+12 \quad \ 36x+12
\end{matrix}</math></center> \end{matrix}</math></center>
 +}}
 +
 +{{p}}
 +{{wolfram desplegable|titulo=División de polinomios|contenido=
 +{{wolfram
 +|titulo=Actividad: ''División de polinomios''
 +|cuerpo=
 +{{ejercicio_cuerpo
 +|enunciado=
 +Calcula el cociente y el resto de la siguiente división de polinomios:
 +
 +:<math>x^3-4x^2+x+6):(x-1)</math>
 +
 +|sol=
 +Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión:
 +
 +{{consulta|texto=quotient and remainder (x^3-4x^2+x+6)/(x-1)}}
 +
 +{{widget generico}}
 +}}
 +}}
}} }}

Revisión de 16:37 26 oct 2016

La división polinómica es, en ciertos aspectos, similar a la división numérica.

Dados dos polinomios 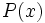P(x)\; (dividendo) y 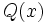Q(x)\; (divisor) de modo que el grado de 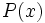P(x)\; sea mayor o igual que el grado de 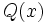Q(x)\; y el grado de 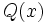Q(x)\; sea mayor o igual a cero, siempre podremos hallar dos polinomios 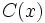C(x)\; (cociente) y 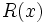R(x)\; (resto) tales que:

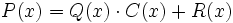
P(x) = Q(x) \cdot C(x)+ R(x) \,
dividendo = divisor × cociente + resto

que también podemos representar como:

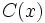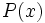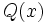  • El grado de C(x)\; es igual a la diferencia entre los grados de P(x)\; y Q(x)\;, mientras que el grado de 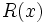R(x)\; será, como máximo, un grado menor que Q(x)\;.
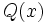  • Cuando el resto sea igual a cero diremos que el dividendo es divisible por el divisor, es decir, que la división es exacta.

ejercicio

Ejemplo: División de polinomios

Divide los siguientes polinomios:

P(x) = 3 \, x^{4} - 2 \, x^{3} + 4 \, x^{2} + 2 \, \, x - 3\;
Q(x) = x^{2} - 2 \, x - 1 \;
Solución:
\begin{matrix} ~~~3x^{4} - 2x^3 + 4x^2 + 2x - 3 \quad | \quad x^{2} - 2 \, x - 1 \quad \\ ~~~\qquad \qquad \qquad \qquad \qquad \qquad \quad \quad \; \, \, \, |-------- \quad \quad \\ -3x^4 + 6x^3 + 3x^2 \qquad \qquad \quad \quad 3x^{2} + 4x +15 \; \, \\ -------- \qquad \qquad \qquad \qquad \qquad \qquad \\ 4x^3 + 7x^2 + 2x -3 \qquad \qquad \quad \\ -4x^3 + 8x^2 + 4x \qquad \qquad \qquad \quad \; \, \\ ---------- \qquad \qquad \qquad \\ ~15x^2 + ~6x -~3 \quad \quad \; \, \\ -15x^2 + 30x + 15 \quad \quad \; \, \, \\ --------- \qquad \quad \\ \quad \ 36x+12 \end{matrix}

wolfram
División de polinomios
wolfram

Actividad: División de polinomios

Calcula el cociente y el resto de la siguiente división de polinomios:

x3 − 4x2 + x + 6):(x − 1)
Solución:
Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión:

quotient and remainder (x^3-4x^2+x+6)/(x-1)

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Divisi%C3%B3n_de_polinomios"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda