Plantilla:Crecimiento y variación de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:12 3 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:41 3 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto= | |texto= | ||
| - | Se llama '''variación''' de una función en un intervalo, a lo que varía la variable dependiente de un extremo a otro del intervalo.}} | + | Se llama '''variación''' de una función <math>f\;</math> en un intervalo <math>[a,b]\;</math>, a lo que varía la variable dependiente de un extremo a otro del intervalo: |
| + | <center><math>\Delta f_{[a,b]}=f(b)-f(a)\;</math></center> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
Revisión de 19:41 3 nov 2016
- Una función es creciente en un tramo cuando al aumentar la variable independiente
 en ese tramo, aumenta la variable dependiente
en ese tramo, aumenta la variable dependiente 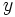 .
.
- Una función es decreciente en un tramo cuando al aumentar la variable independiente
 en ese tramo, disminuye la variable dependiente
en ese tramo, disminuye la variable dependiente 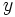 .
.
Se llama variación de una función 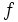 en un intervalo
en un intervalo ![[a,b]\;](/wikipedia/images/math/9/a/e/9ae0a6959368a1b0c6be4a9feb1e9b5c.png) , a lo que varía la variable dependiente de un extremo a otro del intervalo:
, a lo que varía la variable dependiente de un extremo a otro del intervalo:
![\Delta f_{[a,b]}=f(b)-f(a)\;](/wikipedia/images/math/f/1/e/f1ebdfa1d125fb540c0cf9d9b00d9152.png)
En esta escena podrás ver cuando una función es creciente, decreciente o constante.

