Función cuadrática (3ºESO Académicas)
De Wikipedia
| Revisión de 11:38 13 nov 2016 Coordinador (Discusión | contribuciones) (→Representación gráfica de la función cuadrática) ← Ir a diferencia anterior |
Revisión de 11:44 13 nov 2016 Coordinador (Discusión | contribuciones) (→Función cuadrática tipo) Ir a siguiente diferencia → |
||
| Línea 28: | Línea 28: | ||
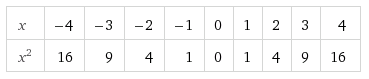
| [[Imagen:tabla_x_2.png|center]] | [[Imagen:tabla_x_2.png|center]] | ||
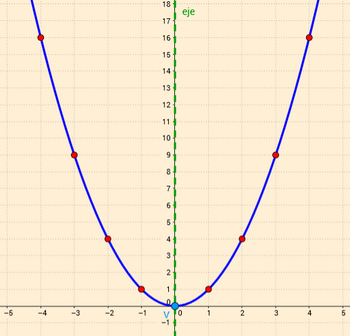
| - | La gráfica obtenida recibe el nombre de '''parábola'''. (ver imagen de la derecha) | + | Los valores de esta tabla los representamos en unos ejes cartesianos a una escala adecuada. (Son los puntos rojos de la imagen de la derecha). |
| - | Fíjate como su gráfica es simétrica. | + | La gráfica obtenida recibe el nombre de '''parábola'''. |
| - | El '''eje''' de simetría (en verde) divide a la parábola en dos '''ramas''' simétricas. | + | *Fíjate como su gráfica es simétrica. |
| - | El eje corta a la parábola en un punto V, llamado '''vértice'''. | + | *El '''eje''' de simetría (en verde) divide a la parábola en dos '''ramas''' simétricas. |
| + | |||
| + | *El eje corta a la parábola en un punto V, llamado '''vértice'''. | ||
| }} | }} | ||
| + | |||
| ===Función cuadrática general=== | ===Función cuadrática general=== | ||
| La gráfica de cualquier otra función cuadrática tiene un aspecto muy parecido a la "parábola tipo" que acabamos de representar. En general, tienen las siguientes características: | La gráfica de cualquier otra función cuadrática tiene un aspecto muy parecido a la "parábola tipo" que acabamos de representar. En general, tienen las siguientes características: | ||
Revisión de 11:44 13 nov 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 171)
Función cuadrática
Una función cuadrática es aquella cuya expresión analítica es o puede ponerse como una ecuación polinómica de segundo grado:
 |
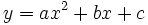con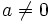 
.
Representación gráfica de la función cuadrática
Función cuadrática tipo
Empezaremos representando la función cuadrática mas sencilla, que llamaremos función cuadrática tipo, cuya ecuación es:
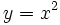 Haremos una tabla de valores y, a partir de ella, dibujaremos su gráfica:  Los valores de esta tabla los representamos en unos ejes cartesianos a una escala adecuada. (Son los puntos rojos de la imagen de la derecha). La gráfica obtenida recibe el nombre de parábola.
|  |
Función cuadrática general
La gráfica de cualquier otra función cuadrática tiene un aspecto muy parecido a la "parábola tipo" que acabamos de representar. En general, tienen las siguientes características:
Propiedades
La representación gráfica de la función cudrática recibe el nombre de parábola y tiene las siguientes propiedades:
- La parábola es simétrica respecto de un eje paralelo al eje Y, que llamaremos eje de la parábola.
- El eje de la parábola corta a la parábola por un punto llamado vértice.
- El eje de la parábola la divide en dos partes denominadas ramas.
- Si
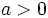, la parábola tiene las ramas hacia arriba.
- Si
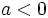, la parábola tiene las ramas hacia abajo.
- Si
- Cuanto mayor es
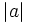, más estilizada es la parábola.
- Dos parábolas con el mismo coeficiente
, tienen formas idénticas aunque están situadas en posiciones distintas.
Ejercicios propuestos
 Ejercicios propuestos: Estudio conjunto de dos funciones lineales (Pág. 171-172)
|
