Ejes de giro (3ºESO Académicas)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:46 1 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:48 1 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| ===Ejes de giro del cubo=== | ===Ejes de giro del cubo=== | ||
| + | {{Tabla50|celda1= | ||
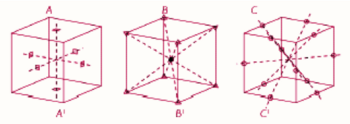
| {{Teorema_sin_demo|titulo=Proposición|enunciado=Un cubo tiene: | {{Teorema_sin_demo|titulo=Proposición|enunciado=Un cubo tiene: | ||
| *3 ejes de giro de orden 4. | *3 ejes de giro de orden 4. | ||
| Línea 20: | Línea 21: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | [[Imagen:ejes_giro_cubo.png|center]] | + | |celda2= |
| + | [[Imagen:ejes_giro_cubo.png|350px|center]] | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| ===Ejes de giro del tetraedro=== | ===Ejes de giro del tetraedro=== | ||
| + | {{Tabla50|celda1= | ||
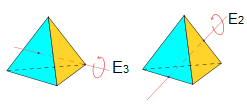
| {{Teorema_sin_demo|titulo=Proposición|enunciado=Un cubo tiene: | {{Teorema_sin_demo|titulo=Proposición|enunciado=Un cubo tiene: | ||
| *4 ejes de giro de orden 3, que pasan por el vértice y el baricentro de la cara opuesta al mismo. | *4 ejes de giro de orden 3, que pasan por el vértice y el baricentro de la cara opuesta al mismo. | ||
| Línea 28: | Línea 32: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |celda2= | ||
| [[Imagen:ejes_tetra.png|center]] | [[Imagen:ejes_tetra.png|center]] | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
Revisión de 17:48 1 dic 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 213)
Ejes de giro
Una recta e es eje de giro de orden n de una figura si, al girar la figura en torno al eje, ésta ocupa la misma posición n veces (incluida la posición inicial).
Ejes de giro del cubo
Ejes de giro del tetraedro
Ejercicios propuestos
|
Ejercicios propuestos: Ejes de giro |