Familias de funciones elementales (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:42 9 dic 2016 Coordinador (Discusión | contribuciones) (→Funciones cuadráticas) ← Ir a diferencia anterior |
Revisión de 18:54 9 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Funciones lineales== | ==Funciones lineales== | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=Representación de la familia de funciones lineales. | ||
| + | |enlace=[https://ggbm.at/Y9r5yYqP La función lineal] | ||
| + | }} | ||
| + | {{p}} | ||
| ==Funciones cuadráticas== | ==Funciones cuadráticas== | ||
Revisión de 18:54 9 dic 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Funciones lineales
Representación de la familia de funciones lineales.
Funciones cuadráticas
Representación de la familia de funciones cuadráticas.
Funciones raíz
Funciones de proporcionalidad inversa
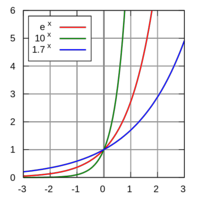
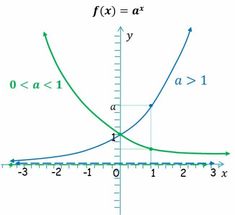
Funciones exponenciales
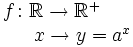
|
Propiedades
Propiedades de la función exponencial Las funciones exponenciales de base
|
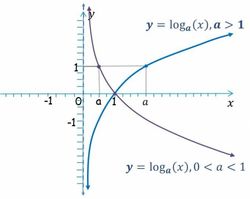
Funciones logarítmicas
Sea 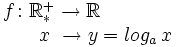
|
Propiedades
Propiedades de la función logarítmica Las funciones exponenciales de base
|
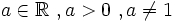 . Se define la función exponencial de base
. Se define la función exponencial de base  como:
como:
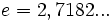 (número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
(número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
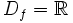 .
.
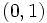 y
y 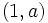 .
.
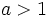 son crecientes
son crecientes
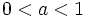 son decrecientes.
son decrecientes.
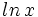 .
.
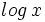 (sin especificar la base).
(sin especificar la base).
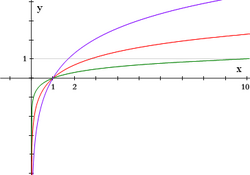
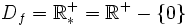 .
.
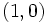 y
y 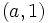 .
.
![\sqrt[n]{x}](/wikipedia/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) .
.
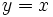 .
.